Programvaretilnærming til å håndtere støynivået til ADAS-sensorer (Del 1)

Hva er ADAS?

Moderne biler blir stadig mer intelligente takket være ADAS (Advanced Driver Assistance Systems) som forbedrer veisikkerheten og gjør kjøring mer komfortabel. Disse systemene, som bruker kameraer, radarer og andre sensorer, bistår i kjøretøykontroll, detekterer andre kjøretøy, fotgjengere og trafikklyssignaler, og gir føreren oppdatert informasjon om veiforholdene og det omkringliggende miljøet.

ADAS inkluderer forskjellige funksjoner som adaptiv cruisekontroll, som justerer bilens hastighet til trafikken foran, kjørefeltsystemer for å holde bilen i sin kjørebane, automatisk bremsing for å forhindre kollisjoner, og automatiske parkeringssystemer for å lette parkeringsmanøvrer. Forskjellige typer sensorer, som kameraer, radarer, lidarer og ultrasoniske sensorer, sikrer at disse systemene fungerer, og hjelper bilen med å tilpasse seg veiforholdene og førerens kjørestil.

Støy i sensorer i ADAS

ADAS-sensorer, til tross for deres modernitet og kompleksitet, er utsatt for støyforstyrrelser. Dette skjer av flere årsaker. For det første kan miljøet ha uforutsigbare effekter på sensorene. For eksempel kan smuss, støv, regn eller snø dekke kameraer og radarer, og forvrenge informasjonen de mottar. Det er som å prøve å se gjennom skittent glass: ikke alt er synlig og ikke så klart, og utsikten er blokkert av mange artefakter. For det andre kan de tekniske begrensningene til selve sensorene også føre til støy. For eksempel kan sensorer utføre dårlig i dårlige lysforhold eller i sterke lyskontraster. Dette er som å prøve å skjelne noe i mørket eller å se på en altfor lys lyskilde – i begge tilfeller blir det ekstremt vanskelig å se detaljer. Når dataene som mottas fra sensorer er forvrengt, kan førerassistansesystemet misforstå veisituasjonen, noe som i visse situasjoner kan øke risikoen for trafikkulykker.

Simulering av punktbevegelse i et eindimensjonalt koordinatsystem

For å starte, la oss skrive koden for å simulere bevegelsen til en bil i et éndimensjonalt rom. For å kjøre koden, må du sette opp et Python-miljø og installere de nødvendige bibliotekene.

Her er trinnene for å installere bibliotekene og kjøre koden:

For å kjøre koden, må du sette opp et Python-miljø og installere nødvendige biblioteker. Her er trinnene for å installere bibliotekene og kjøre koden: Installer Python: Hvis du ikke har Python enda, last ned og installer det fra den offisielle Python-nettsiden (https://www.python.org/downloads/). Det anbefales å bruke Python versjon 3.x.
Installer nødvendige biblioteker: Åpne kommandolinjen (i Windows kan det være kommandoprompten eller PowerShell) og utfør følgende kommando for å installere bibliotekene:
```
pip install matplotlib numpy filterpy
```
Lagre koden din: Kopier koden du har gitt og lagre den i en fil med endelsen .py (for eksempel simulation.py)
Kjør koden: I kommandolinjen, naviger til mappen der kodefilen din ligger og kjør den med følgende kommando:
```
python simulation.py 20 20 500
```
Denne kommandoen vil kjøre koden med argumenter 20 (for støyamplitude), 20 (for støyfrekvens), og 500 (for det totale antall datapunkter på grafen). Du kan endre argumentverdiene etter behov.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
import sys
import random
import time

# Named constants
AMPLITUDE_FACTOR = 5.0  # Factor for amplitude in the nonlinear acceleration function
WAVES = 4  # Number of waves in the nonlinear motion model
INITIAL_POSITION = 0  # Initial position
TRUE_VELOCITY_INITIAL = 2.0  # Initial true velocity (changed to float)
TRUE_VELOCITY_INCREMENT = 0.2  # Increment for true velocity (added as a constant)
PREDICTION_INTERVAL = 10  # Interval for predictions
DIM_X = 2  # Dimension of state vector in Kalman filter
DIM_Z = 1  # Dimension of measurement vector in Kalman filter
INITIAL_P_COVARIANCE = 1000  # Initial state covariance for Kalman filter
RANDOM_SEED = 42  # Seed for random number generator

# Initialize random number generator with the current time
random.seed(int(time.time()))  # Using the current time to initialize the random number generator

# Read noise_percentage, noise_probability, and total_points from command line arguments
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = PREDICTION_INTERVAL / total_points  # Time interval between data points

# Define a nonlinear acceleration function that varies with time
def nonlinear_acceleration(t):
    # Calculate the amplitude of acceleration based on time
    amplitude = AMPLITUDE_FACTOR * 200.0 * (1 - abs((t % (total_points / WAVES) - (total_points / (2 * WAVES))) / (total_points / (2 * WAVES))))
    # Calculate the nonlinear acceleration based on time and amplitude
    return amplitude * np.sin(2.0 * np.pi * t / (total_points / WAVES))

# Function to add noise to true positions with a given probability
def add_noise(true_positions, probability):
    # Add Gaussian noise to true positions with specified probability
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions)) if random.uniform(0, 1) <= probability else p for p in true_positions]

# Function to close the animation on pressing the ESC key
def close_animation(event):
    if event.key == 'escape':
        plt.close()

# Function for creating an animation without the Kalman Filter
def animate_without_ekf(i):
    plt.cla()
    # Plot the true position and sensor data up to the current time
    plt.plot(true_positions_nonlinear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, label='Sensor Data', linewidth=0.5)

    # Set plot limits and labels
    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_nonlinear + sensor_positions_with_noise),
             max(true_positions_nonlinear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Nonlinear One-Dimensional Motion')

    # Display the legend
    plt.legend()

# Main entry point of the code
if __name__ == "__main__":
    # Create a figure for the animation
    fig, ax = plt.subplots(figsize=(10, 6))

    # Use connect to add an event handler for key presses
    fig.canvas.mpl_connect('key_press_event', close_animation)

    # Initialize true_positions_nonlinear with the initial position and true_velocity
    true_positions_nonlinear = [INITIAL_POSITION]
    true_velocity = TRUE_VELOCITY_INITIAL

    # Generate true positions based on the nonlinear motion model
    for t in range(1, total_points):
        acc = nonlinear_acceleration(t)
        true_velocity += acc * interval
        true_positions_nonlinear.append(true_positions_nonlinear[-1] + true_velocity * interval)

    # Add noise to true positions to simulate sensor data
    sensor_positions_with_noise = add_noise(true_positions_nonlinear, noise_probability)

    # Create the animation using FuncAnimation
    ani = FuncAnimation(fig, animate_without_ekf, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

Dette er en simulering av en bils bevegelse i ett-dimensjonalt rom:

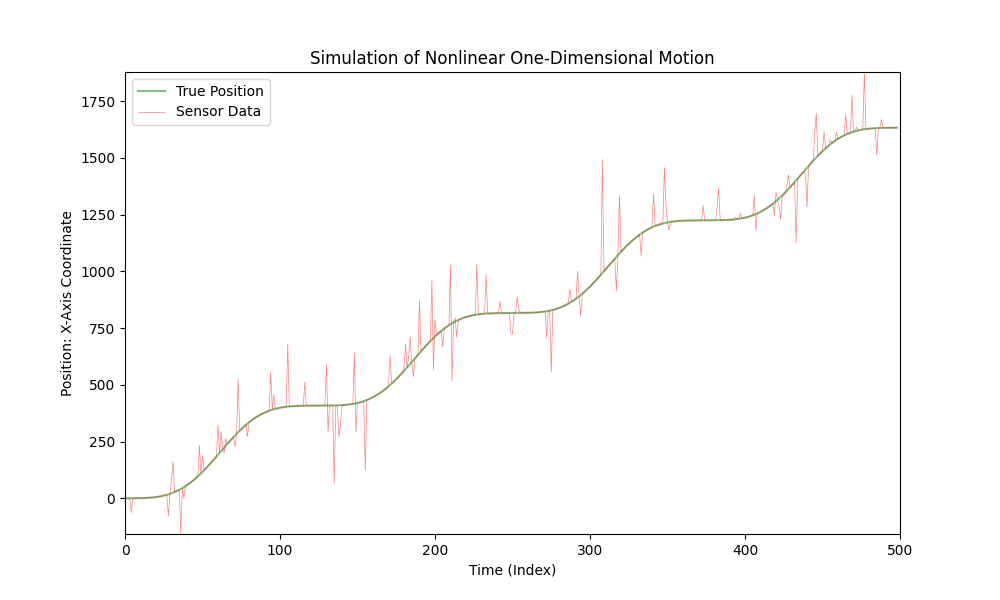
Bilen beveger seg med variabel akselerasjon, og en sensor måler bilens X-koordinat. I denne simuleringen tilføyer vi støy til sensordataene for å ta hensyn til mulige målefeil.

Koden som ble gitt tidligere visualiserer denne simuleringen, der den grønne linjen representerer bilens "sanne" posisjon, og den røde linjen representerer sensordataene, med tanke på den tilføyde støyen. Akselerasjonen endres over tid, noe som skaper en mer realistisk simulering av bilens bevegelse.

Denne koden kan brukes for å visualisere og analysere ulike scenarioer av bilbevegelse, med tanke på endrende akselerasjon og mulige sensorfeil.

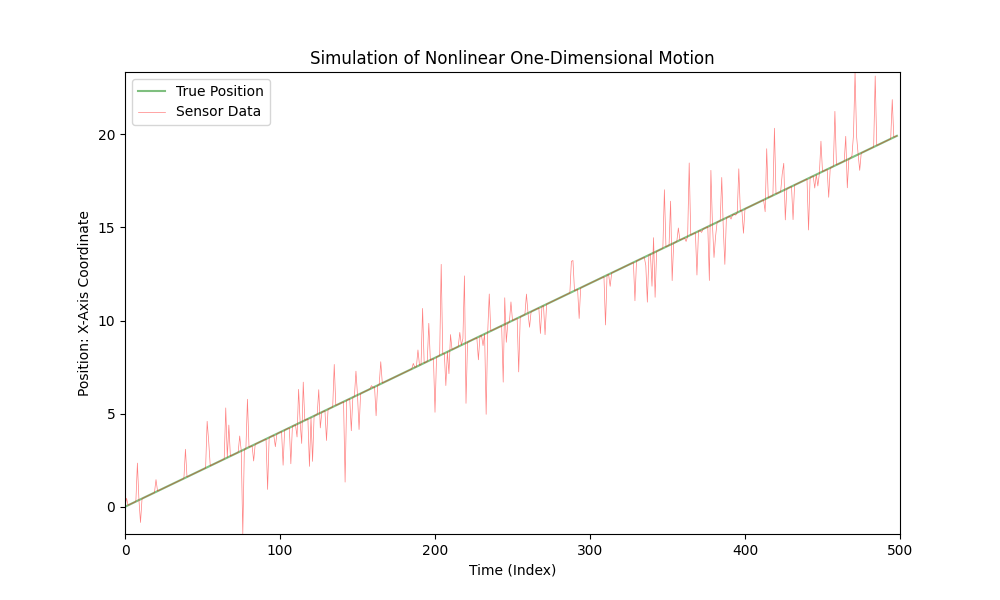
For å simulere lineær bevegelse, kan du enkelt endre nonlinear_acceleration(t) funksjonen til alltid å returnere 0:

def nonlinear_acceleration(t):
    return 0

Denne endringen vil gjøre bilens bevegelse lineær med konstant hastighet.

Kalman-filteret

Kalman-filteret er en algoritme utviklet av Rudolf E. Kalman i 1960. Denne algoritmen muliggjør estimering av tilstanden til et dynamisk system basert på et sett med ufullstendige og støyende målinger. Opprinnelig ble Kalman-filteret utviklet for å løse problemer innen romfartsteknologi, men over tid har det funnet bred anvendelse i forskjellige felt. Hovedfordelen med Kalman-filteret er at det er rekursivt, noe som betyr at det bruker de siste målingene og den forrige tilstanden til å beregne systemets nåværende tilstand. Dette gjør det effektivt for online sanntids databehandling.

Kalman-filteret har funnet anvendelser innen mange felt, inkludert navigasjon og kjøretøykontroll, signalbehandling, økonometri, robotikk, og mange andre områder der estimering av tidsvarierende prosesser basert på uperfekte eller ufullstendige data er nødvendig.

Kalman-filteret har flere nøkkel fordeler sammenlignet med andre algoritmer for dataestimering og filtrering:

Optimalitet: Under visse forhold (lineært system, Gaussisk støy), er Kalman-filteret optimalt med tanke på å minimere gjennomsnittlig kvadrert estimeringsfeil.
Effektivitet i sanntid: Kalman-filteret er rekursivt, noe som betyr at det kun bruker de siste målingene og den forrige tilstanden for å beregne den nåværende tilstanden. Dette gjør det egnet for sanntidsapplikasjoner.
Minimalt minnekrav: Siden filteret kun bruker den nyeste målingen og den nåværende tilstandsestimatet, trenger det ikke å lagre hele historikken med data.
Robusthet mot målefeil: Filteret er i stand til effektivt å behandle støyende data, og minimerer effekten av tilfeldige målefeil.
Versatile applikasjoner: På grunn av sin allsidighet, har Kalman-filteret blitt brukt i mange forskjellige felt, fra romfartsteknikk til økonometri.
Enkel implementering: Algoritmen er relativt enkel å forstå og implementere, noe som gjør den tilgjengelig for et bredt spekter av profesjonelle.

La oss implementere et grunnleggende Kalman-filter for en sensor som måler posisjonen til bilen vår, som beveger seg i et endimensjonalt system med konstant hastighet, men med støyende sensoravlesninger.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
import sys
import random

# Read noise_percentage, noise_probability, total_points from the command line
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = 10 / total_points

# Initialize true positions and velocity
true_positions_linear = [0]
true_velocity = 2

for t in range(1, total_points):
    true_positions_linear.append(true_positions_linear[-1] + true_velocity * interval)

# Function to add noise to true positions
def add_noise(true_positions, probability):
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions))
            if random.uniform(0, 1) <= probability else p for p in true_positions]

sensor_positions_with_noise = add_noise(true_positions_linear, noise_probability)

# Initialize Kalman Filter (KF)
kf = KalmanFilter(dim_x=2, dim_z=1)
kf.F = np.array([[1, interval],
                 [0, 1]])
kf.H = np.array([[1, 0]])
kf.P *= 1000
kf.R = noise_percentage * np.mean(true_positions_linear)
kf.Q = Q_discrete_white_noise(dim=2, dt=interval, var=0.001)

x = np.array([[sensor_positions_with_noise[0]],
              [0]])
kf_positions = [x[0, 0]]

# Function to update Kalman Filter with sensor data
def update_kalman_filter(z):
    kf.predict()
    kf.update(z)
    return kf.x[0, 0]

# Function to create an animation with Kalman Filter (KF) estimation
def animate_with_kalman(i):
    plt.cla()
    plt.plot(true_positions_linear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, linewidth=0.5, label='Sensor Data')

    if i < total_points:
        kf_estimate = update_kalman_filter(sensor_positions_with_noise[i])
        kf_positions.append(kf_estimate)

    plt.plot(kf_positions[:i + 1], color='blue', alpha=0.5, label='Kalman Filter (KF) Estimate')

    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_linear + sensor_positions_with_noise),
             max(true_positions_linear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Linear One-Dimensional Motion with Kalman Filter (KF)')
    plt.legend()

# Main entry point
if __name__ == "__main__":
    # Create a figure and animation
    fig, ax = plt.subplots(figsize=(10, 6))
    ani = FuncAnimation(fig, animate_with_kalman, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

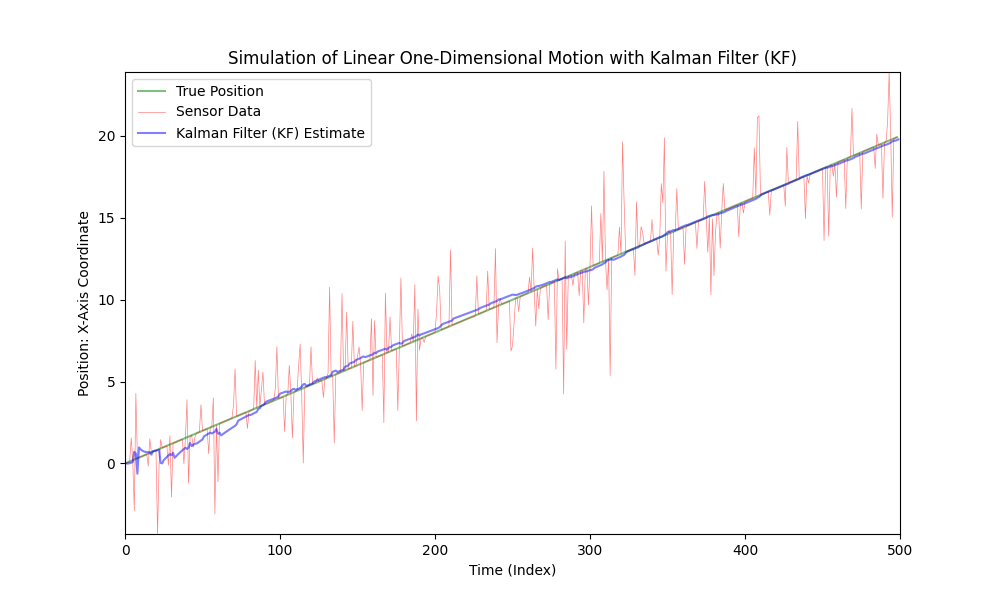
Som sett, er Kalman Filter godt egnet for bruk i lineære systemer selv med sterk støy. Imidlertid er ikke bilens bevegelse lineær; bilen akselererer med varierende størrelser og retninger.

La oss komplisere koden vår litt ved å gjøre bilens bevegelse ikke-lineær og innføre variabel akselerasjon. For enkelhets skyld og tydelighet, vil vi bruke en sinusfunksjon for å modellere akselerasjonen. Vi vil holde støynivået det samme.

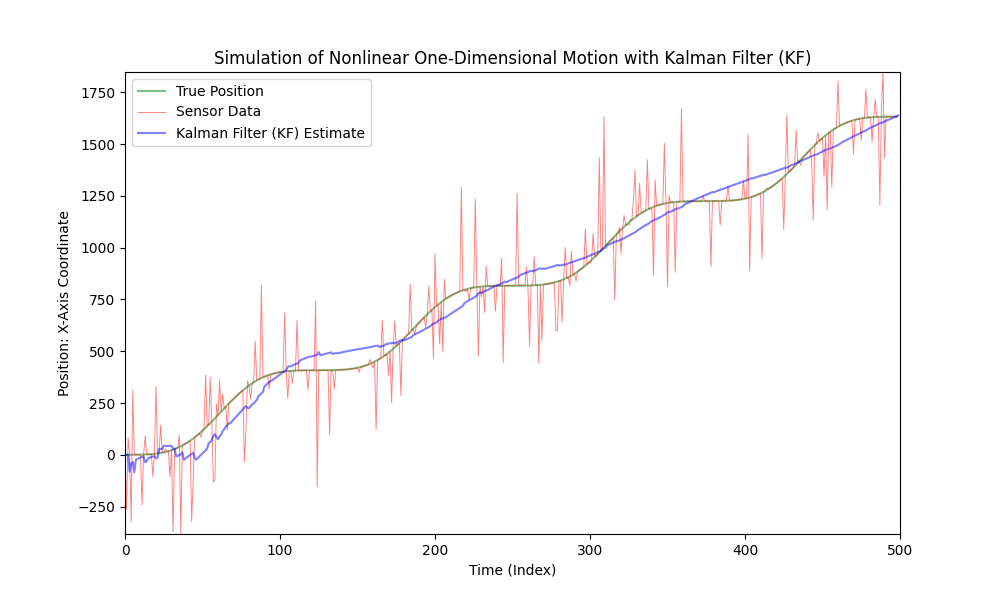
Som vi kan se, er den klassiske Kalman Filter ikke egnet for ikke-lineære modeller. For disse formålene ble Extended Kalman Filter (EKF) utviklet.

Utvidet Kalman-filter (EKF)

Den utvidede Kalman-filteret (EKF) er en modifikasjon av det klassiske Kalman-filteret designet for å fungere med ikke-lineære systemer. Mens det standard Kalman-filteret er ment for lineære systemer, utvider EKF dens anvendelighet til å håndtere ikke-lineære tilfeller.

Den utvidede Kalman-filteret ble utviklet etter det originale Kalman-filteret, introdusert av Rudolf Kalman i 1960. Det oppsto som et resultat av anstrengelser fra ingeniører og vitenskapsmenn for å tilpasse Kalman-filteret for bruk med ikke-lineære systemer, spesielt innen luftfart og marin navigasjon på 1960- og 1970-tallet. Den nøyaktige datoen for dets opprettelse og spesifikke forfattere er mindre kjent, ettersom EKF utviklet seg gradvis og innenfor rammen av forskjellige forskningsgrupper.

Extended Kalman Filter (EKF) brukes mye i oppgaver hvor tilstandsestimering av systemer beskrevet av ikke-lineære ligninger er nødvendig. De viktigste anvendelsesområdene inkluderer robotikk (for estimering av posisjon og orientering av roboter), bilindustrien (i autonome kjøresystemer og navigasjon), romfartsteknikk (for navigasjon av satellittbaner og romfartøy), mobilkommunikasjon og mange andre tekniske og ingeniørfaglige felt.

De viktigste forskjellene mellom Extended Kalman Filter (EKF) og standard Kalman Filter ligger hovedsakelig i hvordan de håndterer dynamikken og målingene av systemet.

De primære forskjellene inkluderer følgende:

Håndtering av ikke-linearitet: Den standard Kalman-filteret antar at systemdynamikken og måleprosessen er lineære. Dette betyr at tilstandsovergangs- og målingsfunksjonene kan representeres som lineære matriser. Det utvidede Kalman-filteret (EKF) er designet for å fungere med ikke-lineære systemer. I stedet for lineære matriser, bruker det ikke-lineære funksjoner for å beskrive systemdynamikken og måleprosessen.
Linearisering: I EKF brukes linearisering for å tilnærme ikke-lineære funksjoner, vanligvis gjennom førsteordens Taylor-serieekspansjon rundt den nåværende tilstandsestimatet. Dette gir lineariserte motparter av tilstandsovergangs- og målingsfunksjonene, som deretter brukes i filteret.
Tilstandsovergangs- og målingsfunksjoner: I det standard Kalman-filteret representeres tilstandsovergangs- og målingsfunksjonene ved matriser (f.eks. tilstandsovergangsmatrise og målematrise). I EKF kan disse funksjonene være hvilke som helst differensierbare ikke-lineære funksjoner. Dette tilføyer fleksibilitet, men øker også kompleksiteten og de beregningsmessige kravene.
Beregningskompleksitet: EKF krever høyere beregningskompleksitet på grunn av behovet for å linearisere ikke-lineære funksjoner og påfølgende beregninger.

Hovedforskjellen mellom Extended Kalman Filter og det standard er dets evne til å håndtere ikke-lineære systemer ved å bruke ikke-lineære funksjoner og deres linearisering.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
import sys
import random

# Named constants
AMPLITUDE_FACTOR = 5.0  # Factor for amplitude in the nonlinear acceleration function
WAVES = 4  # Number of waves in the nonlinear motion model
INITIAL_POSITION = 0  # Initial position
TRUE_VELOCITY_INITIAL = 2.0  # Initial true velocity (changed to float)
TRUE_VELOCITY_INCREMENT = 0.2  # Increment for true velocity (added as a constant)
PREDICTION_INTERVAL = 10  # Interval for predictions
DIM_X = 2  # Dimension of state vector in Kalman filter
DIM_Z = 1  # Dimension of measurement vector in Kalman filter
INITIAL_P_COVARIANCE = 1000  # Initial state covariance for Kalman filter

# Initialize random number generator with the current time
random.seed()

# Read noise_percentage, noise_probability, and total_points from command line arguments
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = PREDICTION_INTERVAL / total_points  # Time interval between data points

# Define a nonlinear acceleration function that varies with time
def nonlinear_acceleration(t):
    # Calculate the amplitude of acceleration based on time
    amplitude = AMPLITUDE_FACTOR * 200.0 * (1 - abs((t % (total_points / WAVES) - (total_points / (2 * WAVES))) / (total_points / (2 * WAVES))))
    # Calculate the nonlinear acceleration based on time and amplitude
    return amplitude * np.sin(2.0 * np.pi * t / (total_points / WAVES))

# Function to add noise to true positions with a given probability
def add_noise(true_positions, probability):
    # Add Gaussian noise to true positions with specified probability
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions)) if random.uniform(0, 1) <= probability else p for p in true_positions]

# Function to update the Extended Kalman Filter (EKF) with sensor measurements
def update_extended_kalman_filter(z):
    ekf.predict()  # Predict the next state
    ekf.update(z)  # Update the state based on sensor measurements
    return ekf.x[0, 0]  # Return the estimated position

# Функция для закрытия анимации при нажатии клавиши ESC
def close_animation(event):
    if event.key == 'escape':
        plt.close()

# Function for creating an animation with EKF estimates
def animate_with_ekf(i):
    plt.cla()
    # Plot the true position and sensor data up to the current time
    plt.plot(true_positions_nonlinear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, label='Sensor Data', linewidth=0.5)

    if i < total_points:
        # Update the EKF with the current sensor measurement and obtain the estimate
        ekf_estimate = update_extended_kalman_filter(sensor_positions_with_noise[i])
        ekf_positions.append(ekf_estimate)

    # Plot the EKF estimate up to the current time
    plt.plot(ekf_positions[:i + 1], color='purple', alpha=0.5, label='Extended Kalman Filter (EKF) Estimate')

    # Set plot limits and labels
    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_nonlinear + sensor_positions_with_noise),
             max(true_positions_nonlinear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Nonlinear One-Dimensional Motion with Extended Kalman Filter (EKF)')
    plt.legend()

# Main entry point of the code
if __name__ == "__main__":
    # Create a figure for the animation
    fig, ax = plt.subplots(figsize=(10, 6))

    # Используйте connect для добавления обработчика событий
    fig.canvas.mpl_connect('key_press_event', close_animation)

    # Initialize true_positions_nonlinear with the initial position and true_velocity
    true_positions_nonlinear = [INITIAL_POSITION]
    true_velocity = TRUE_VELOCITY_INITIAL

    # Generate true positions based on the nonlinear motion model
    for t in range(1, total_points):
        acc = nonlinear_acceleration(t)
        true_velocity += acc * interval
        true_positions_nonlinear.append(true_positions_nonlinear[-1] + true_velocity * interval)

    # Add noise to true positions to simulate sensor data
    sensor_positions_with_noise = add_noise(true_positions_nonlinear, noise_probability)

    # Initialize an Extended Kalman Filter (EKF)
    ekf = KalmanFilter(dim_x=DIM_X, dim_z=DIM_Z)
    ekf.F = np.array([[1, interval],
                    [0, 1]])
    ekf.H = np.array([[1, 0]])
    ekf.P *= INITIAL_P_COVARIANCE
    ekf.R = noise_percentage * np.mean(true_positions_nonlinear)

    ekf_x = np.array([[sensor_positions_with_noise[0]],
                    [0]])
    ekf_positions = [ekf_x[0, 0]]

    # Create the animation using FuncAnimation
    ani = FuncAnimation(fig, animate_with_ekf, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

Bruk Extended Kalman Filter for ikke-lineær bevegelse.

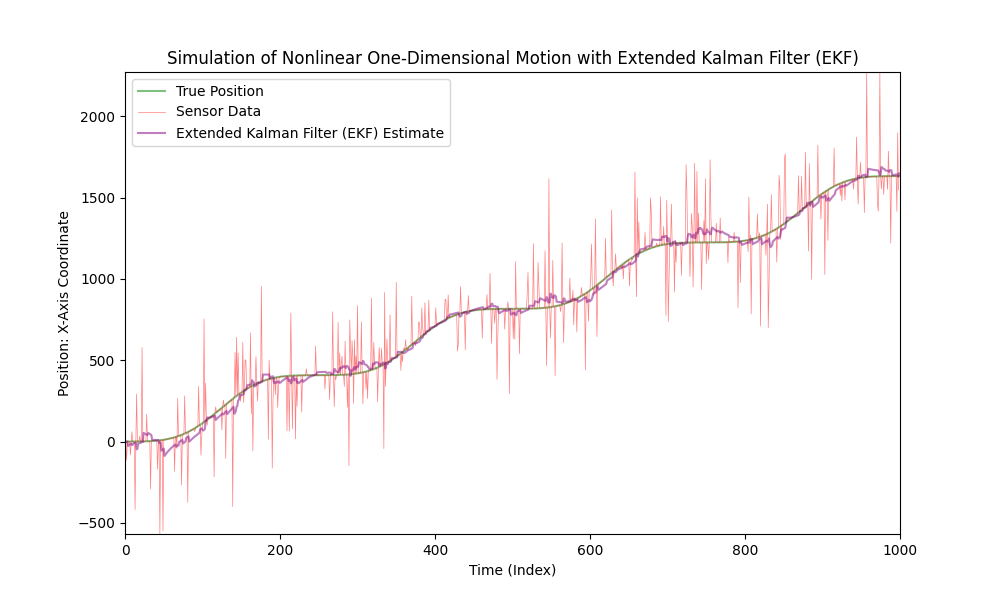
Nå, la oss betydelig øke nivået av sensorstøy.

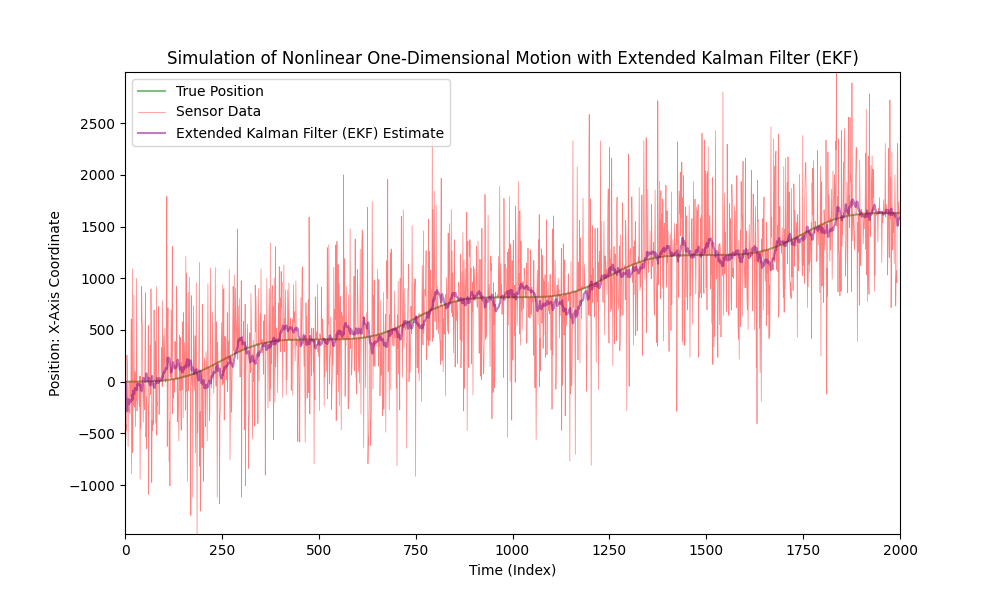
Som vi kan se, utfører Extended Kalman Filter godt selv i tilfeller med svært støyende data.

Ekstra materialer

https://en.wikipedia.org/wiki/Kalman_filter - Beskrivelse av filteret og dets grunnleggende matematiske prinsipper for drift.

https://kalmanfilter.org/cpp/index.html - Beskrivelse og implementering av filteret i C++.

https://commons.apache.org/proper/commons-math/javadocs/api-3.6.1/org/apache/commons/math3/filter/KalmanFilter.html - Beskrivelse og implementasjon av filteret i Java.

https://filterpy.readthedocs.io/en/latest/kalman/KalmanFilter.html - Beskrivelse og implementasjon av filteret i Python

Konklusjon

Extended Kalman Filter (EKF) er et kraftig verktøy for å estimere tilstanden til dynamiske systemer, spesielt når denne estimeringen må baseres på data fra flere sensorer samtidig. En av de viktigste fordelene med EKF er dens evne til å integrere informasjon fra forskjellige kilder, noe som gjør den eksepsjonelt nyttig i komplekse systemer som bilnavigasjonssystemer, robotikk eller romfartsteknikk.

Med tanke på støyende og ofte uperfekte data fra ulike sensorer, er EKF i stand til å slå sammen disse dataene til en enhetlig helhet, noe som gir en mer nøyaktig og pålitelig tilstandsvurdering. For eksempel, i en bil, kan EKF bruke GPS-data for å bestemme posisjon og akselerometerdata for å beregne fart og akselerasjon, og dermed skape et mer komplett bilde av kjøretøyets bevegelse.

Den Utvidede Kalman Filteret (EKF) er i stand til å redusere den samlede usikkerheten som oppstår fra støy og feil fra hver enkelt sensor. Siden disse feilene ofte er ukorrelerte, muliggjør deres felles behandling i EKF mer stabile og nøyaktige estimater. Det er også verdt å merke seg at EKF viser høy robusthet: i tilfelle problemer med en av sensorene, kan systemet fortsette å fungere ved å stole på data fra de gjenværende. Dette gjør EKF spesielt verdifull i kritiske applikasjoner hvor pålitelighet og nøyaktighet er av største betydning. Et annet viktig aspekt ved arbeid med flere sensorer er tids-synkronisering av målinger. EKF håndterer dyktig disse tidsforskjellene, og sikrer korrekt datafusjon.

Takket være sin evne til å aggregere og analysere informasjon fra flere kilder, er EKF et uvurderlig verktøy i områder der det kreves høy presisjons tilstandsestimering under forhold med usikkerhet og dynamiske endringer.

Avslutningsvis er programvare som bekjemper sensorstøy en utfordrende prosess som omfatter statiske, statistiske metoder og bruk av kunstig intelligens for klassifisering og reduksjon av støytyper.

Vårt selskap har betydelig ekspertise i å håndtere problemer med sensorstøy.

For henvendelser angående denne artikkelen, kan du gjerne kontakte oss på articles@stofu.io.

For samarbeidsmuligheter kan du kontakte oss på info@stofu.io.

Alle kodefiler finner du i vårt repositorium: https://github.com/SToFU-Systems/EKF_Usage.

Ønsker deg alt det beste,

SToFU Systems Team

https://stofu.io

Programvaretilnærming til å håndtere støynivået til ADAS-sensorer (Del 1)

Hva er ADAS?

Støy i sensorer i ADAS

Simulering av punktbevegelse i et eindimensjonalt koordinatsystem

Kalman-filteret

Utvidet Kalman-filter (EKF)

Ekstra materialer

Konklusjon

Kategorier

Nylige nyheter

Programvaretilnærming til å håndtere støynivået til ADAS-sensorer (Del 1)

PE-ressursanalyser i C++ (Naturlig)

Innføring i Windows Kjerneutvikling på Rust (Del 1)

Innføring i GPU-programmering

Inne i BlackMatter: Teknisk Analyse av BlackMatter Løsepengevirus