Softwareansatz zur Bewältigung von ADAS-Sensorgeräuschen (Teil 1)

Was ist ADAS?

Moderne Autos werden dank ADAS (Advanced Driver Assistance Systems) immer intelligenter, was die Verkehrssicherheit erhöht und das Fahren komfortabler macht. Diese Systeme, die Kameras, Radare und andere Sensoren nutzen, unterstützen bei der Fahrzeugkontrolle, erkennen andere Fahrzeuge, Fußgänger und Ampelsignale, und versorgen den Fahrer mit aktuellen Informationen über die Straßenbedingungen und die Umgebung.

ADAS umfasst verschiedene Funktionen wie adaptiven Tempomat, der die Geschwindigkeit des Autos dem vorausfahrenden Verkehr anpasst, Spurhaltungssysteme, um das Auto in seiner Spur zu halten, automatisches Bremsen zur Vermeidung von Kollisionen und automatische Parksysteme zur Erleichterung von Parkmanövern. Verschiedene Arten von Sensoren, wie Kameras, Radare, Lidare und Ultraschallsensoren, gewährleisten die Funktionsfähigkeit dieser Systeme und helfen dem Auto, sich an die Straßenbedingungen und den Fahrstil des Fahrers anzupassen.

Sensorrauschen in ADAS

ADAS-Sensoren sind trotz ihrer Modernität und Komplexität anfällig für Störgeräusche. Dies geschieht aus mehreren Gründen. Erstens können die Umgebungseinflüsse die Sensoren auf unvorhersehbare Weise beeinträchtigen. Beispielsweise können Schmutz, Staub, Regen oder Schnee Kameras und Radare bedecken, wodurch die von ihnen empfangenen Informationen verzerrt werden. Es ist wie der Versuch, durch schmutziges Glas zu schauen: Nicht alles ist sichtbar und nicht so klar, und die Sicht wird durch viele Artefakte behindert. Zweitens können auch die technischen Beschränkungen der Sensoren selbst zu Störgeräuschen führen. Zum Beispiel können Sensoren bei schlechten Lichtverhältnissen oder bei starken Lichtkontrasten schlecht funktionieren. Dies ist vergleichbar mit dem Versuch, etwas im Dunkeln zu erkennen oder in eine übermäßig helle Lichtquelle zu schauen - in beiden Fällen wird es extrem schwierig, Details zu sehen. Wenn die von den Sensoren empfangenen Daten verzerrt sind, kann das Fahrerassistenzsystem die Straßensituation falsch interpretieren, was in bestimmten Situationen das Risiko von Verkehrsunfällen erhöhen kann.

Simulation der Punktverschiebung in einem eindimensionalen Koordinatensystem

Um zu beginnen, schreiben wir den Code zur Simulation der Bewegung eines Autos im eindimensionalen Raum. Um den Code auszuführen, müssen Sie eine Python-Umgebung einrichten und die notwendigen Bibliotheken installieren.

Hier sind die Schritte zur Installation der Bibliotheken und zur Ausführung des Codes:

Um den Code auszuführen, müssen Sie eine Python-Umgebung einrichten und die notwendigen Bibliotheken installieren. Hier sind die Schritte zum Installieren der Bibliotheken und zum Ausführen des Codes: Python installieren: Wenn Sie Python noch nicht haben, laden Sie es von der offiziellen Python-Website herunter und installieren Sie es (https://www.python.org/downloads/). Es wird empfohlen, die Python-Version 3.x zu verwenden.
Installieren Sie die notwendigen Bibliotheken: Öffnen Sie die Kommandozeile (unter Windows könnte das die Eingabeaufforderung oder PowerShell sein) und führen Sie den folgenden Befehl aus, um die Bibliotheken zu installieren:
```
pip install matplotlib numpy filterpy
```
Speichern Sie Ihren Code: Kopieren Sie den von Ihnen bereitgestellten Code und speichern Sie ihn in einer Datei mit der Erweiterung .py (zum Beispiel simulation.py)
Führen Sie den Code aus: Navigieren Sie in der Kommandozeile zum Verzeichnis, in dem sich Ihre Code-Datei befindet, und führen Sie ihn mit dem folgenden Befehl aus:
```
python simulation.py 20 20 500
```
Dieser Befehl wird den Code mit den Argumenten 20 (für die Rauschamplitude), 20 (für die Rauschfrequenz) und 500 (für die Gesamtanzahl der Datenpunkte auf dem Diagramm) ausführen. Sie können die Argumentwerte bei Bedarf ändern.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
import sys
import random
import time

# Named constants
AMPLITUDE_FACTOR = 5.0  # Factor for amplitude in the nonlinear acceleration function
WAVES = 4  # Number of waves in the nonlinear motion model
INITIAL_POSITION = 0  # Initial position
TRUE_VELOCITY_INITIAL = 2.0  # Initial true velocity (changed to float)
TRUE_VELOCITY_INCREMENT = 0.2  # Increment for true velocity (added as a constant)
PREDICTION_INTERVAL = 10  # Interval for predictions
DIM_X = 2  # Dimension of state vector in Kalman filter
DIM_Z = 1  # Dimension of measurement vector in Kalman filter
INITIAL_P_COVARIANCE = 1000  # Initial state covariance for Kalman filter
RANDOM_SEED = 42  # Seed for random number generator

# Initialize random number generator with the current time
random.seed(int(time.time()))  # Using the current time to initialize the random number generator

# Read noise_percentage, noise_probability, and total_points from command line arguments
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = PREDICTION_INTERVAL / total_points  # Time interval between data points

# Define a nonlinear acceleration function that varies with time
def nonlinear_acceleration(t):
    # Calculate the amplitude of acceleration based on time
    amplitude = AMPLITUDE_FACTOR * 200.0 * (1 - abs((t % (total_points / WAVES) - (total_points / (2 * WAVES))) / (total_points / (2 * WAVES))))
    # Calculate the nonlinear acceleration based on time and amplitude
    return amplitude * np.sin(2.0 * np.pi * t / (total_points / WAVES))

# Function to add noise to true positions with a given probability
def add_noise(true_positions, probability):
    # Add Gaussian noise to true positions with specified probability
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions)) if random.uniform(0, 1) <= probability else p for p in true_positions]

# Function to close the animation on pressing the ESC key
def close_animation(event):
    if event.key == 'escape':
        plt.close()

# Function for creating an animation without the Kalman Filter
def animate_without_ekf(i):
    plt.cla()
    # Plot the true position and sensor data up to the current time
    plt.plot(true_positions_nonlinear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, label='Sensor Data', linewidth=0.5)

    # Set plot limits and labels
    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_nonlinear + sensor_positions_with_noise),
             max(true_positions_nonlinear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Nonlinear One-Dimensional Motion')

    # Display the legend
    plt.legend()

# Main entry point of the code
if __name__ == "__main__":
    # Create a figure for the animation
    fig, ax = plt.subplots(figsize=(10, 6))

    # Use connect to add an event handler for key presses
    fig.canvas.mpl_connect('key_press_event', close_animation)

    # Initialize true_positions_nonlinear with the initial position and true_velocity
    true_positions_nonlinear = [INITIAL_POSITION]
    true_velocity = TRUE_VELOCITY_INITIAL

    # Generate true positions based on the nonlinear motion model
    for t in range(1, total_points):
        acc = nonlinear_acceleration(t)
        true_velocity += acc * interval
        true_positions_nonlinear.append(true_positions_nonlinear[-1] + true_velocity * interval)

    # Add noise to true positions to simulate sensor data
    sensor_positions_with_noise = add_noise(true_positions_nonlinear, noise_probability)

    # Create the animation using FuncAnimation
    ani = FuncAnimation(fig, animate_without_ekf, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

Dies ist eine Simulation der Bewegung eines Autos im eindimensionalen Raum:

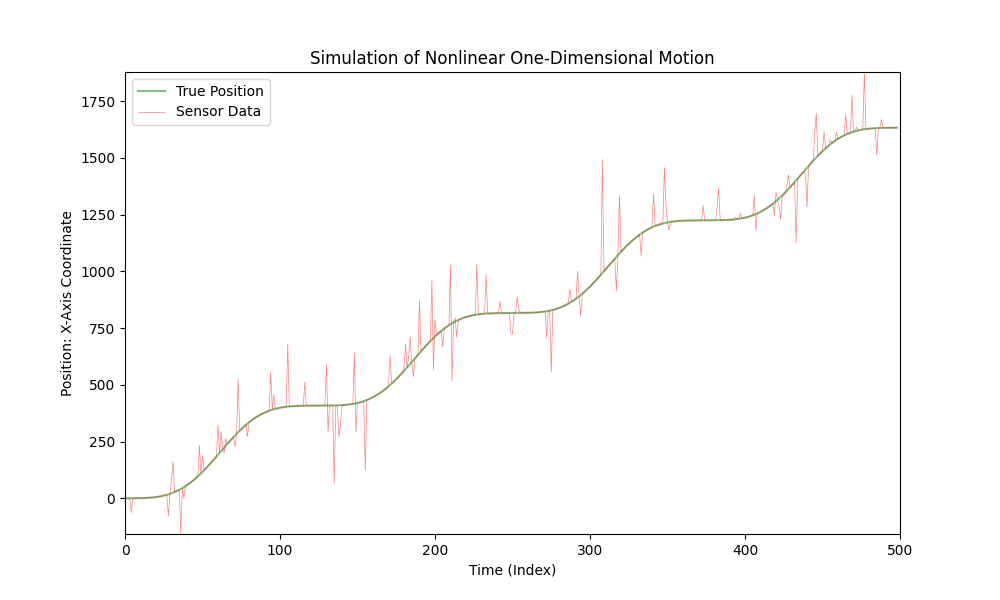
Das Auto bewegt sich mit unterschiedlicher Beschleunigung, und ein Sensor misst die X-Koordinate des Autos. In dieser Simulation fügen wir den Sensordaten Rauschen hinzu, um mögliche Messfehler zu berücksichtigen.

Der zuvor bereitgestellte Code visualisiert diese Simulation, bei der die grüne Linie die "wahre" Position des Autos darstellt und die rote Linie die Sensordaten repräsentiert, unter Berücksichtigung des hinzugefügten Rauschens. Die Beschleunigung verändert sich über die Zeit, was eine realistischere Simulation der Bewegung des Autos ermöglicht.

Dieser Code kann verwendet werden, um verschiedene Szenarien der Bewegung von Autos zu visualisieren und zu analysieren, unter Berücksichtigung von sich ändernder Beschleunigung und möglichen Sensorfehlern.

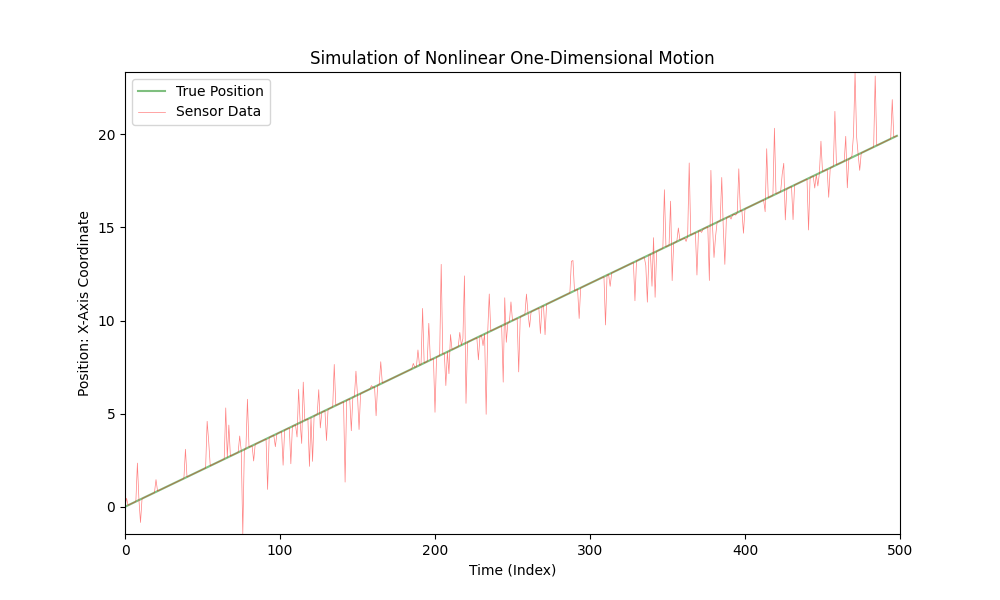
Um lineare Bewegung zu simulieren, können Sie einfach die Funktion nonlinear_acceleration(t) so modifizieren, dass sie immer 0 zurückgibt:

def nonlinear_acceleration(t):
    return 0

Diese Änderung wird die Bewegung des Autos linear mit konstanter Geschwindigkeit machen.

Der Kalman-Filter

Der Kalman-Filter ist ein Algorithmus, der 1960 von Rudolf E. Kalman entwickelt wurde. Dieser Algorithmus ermöglicht die Schätzung des Zustands eines dynamischen Systems basierend auf einer Reihe unvollständiger und verrauschter Messungen. Ursprünglich wurde der Kalman-Filter entwickelt, um Probleme im Bereich der Luft- und Raumfahrttechnik zu adressieren, aber im Laufe der Zeit hat er weite Anwendung in verschiedenen Bereichen gefunden. Der Hauptvorteil des Kalman-Filters ist, dass er rekursiv ist, was bedeutet, dass er die neuesten Messungen und den vorherigen Zustand verwendet, um den aktuellen Zustand des Systems zu berechnen. Dies macht ihn effizient für die Online-Echtzeit-Datenverarbeitung.

Der Kalman-Filter hat Anwendungen in vielen Bereichen gefunden, einschließlich Navigation und Fahrzeugsteuerung, Signalverarbeitung, Ökonometrie, Robotik und vielen anderen Bereichen, in denen die Schätzung von zeitvariablen Prozessen basierend auf unvollständigen oder unvollkommenen Daten erforderlich ist.

Der Kalman-Filter bietet gegenüber anderen Datenabschätzungs- und Filteralgorithmen mehrere entscheidende Vorteile:

Optimalität: Unter bestimmten Bedingungen (lineares System, Gaußsches Rauschen) ist der Kalman-Filter optimal hinsichtlich der Minimierung des mittleren quadratischen Schätzfehlers.
Echtzeiteffizienz: Der Kalman-Filter ist rekursiv, was bedeutet, dass er nur die neuesten Messungen und den vorherigen Zustand verwendet, um den aktuellen Zustand zu berechnen. Dies macht ihn geeignet für Echtzeitanwendungen.
Minimaler Speicherbedarf: Da der Filter nur die neueste Messung und die aktuelle Zustandsschätzung verwendet, muss er nicht die gesamte Datengeschichte speichern.
Robustheit gegen Messfehler: Der Filter kann effizient mit verrauschten Daten umgehen und minimiert die Auswirkungen von zufälligen Messfehlern.
Vielseitige Anwendungen: Aufgrund seiner Vielseitigkeit wurde der Kalman-Filter in verschiedenen Bereichen eingesetzt, von der Luft- und Raumfahrttechnik bis zur Ökonometrie.
Einfache Implementierung: Der Algorithmus ist relativ einfach zu verstehen und zu implementieren, was ihn für eine breite Palette von Fachleuten zugänglich macht.

Lassen wir einen grundlegenden Kalman-Filter für einen Sensor implementieren, der die Position unseres Autos misst, das sich in einem eindimensionalen System mit konstanter Geschwindigkeit bewegt, jedoch mit verrauschten Sensormessungen.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
import sys
import random

# Read noise_percentage, noise_probability, total_points from the command line
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = 10 / total_points

# Initialize true positions and velocity
true_positions_linear = [0]
true_velocity = 2

for t in range(1, total_points):
    true_positions_linear.append(true_positions_linear[-1] + true_velocity * interval)

# Function to add noise to true positions
def add_noise(true_positions, probability):
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions))
            if random.uniform(0, 1) <= probability else p for p in true_positions]

sensor_positions_with_noise = add_noise(true_positions_linear, noise_probability)

# Initialize Kalman Filter (KF)
kf = KalmanFilter(dim_x=2, dim_z=1)
kf.F = np.array([[1, interval],
                 [0, 1]])
kf.H = np.array([[1, 0]])
kf.P *= 1000
kf.R = noise_percentage * np.mean(true_positions_linear)
kf.Q = Q_discrete_white_noise(dim=2, dt=interval, var=0.001)

x = np.array([[sensor_positions_with_noise[0]],
              [0]])
kf_positions = [x[0, 0]]

# Function to update Kalman Filter with sensor data
def update_kalman_filter(z):
    kf.predict()
    kf.update(z)
    return kf.x[0, 0]

# Function to create an animation with Kalman Filter (KF) estimation
def animate_with_kalman(i):
    plt.cla()
    plt.plot(true_positions_linear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, linewidth=0.5, label='Sensor Data')

    if i < total_points:
        kf_estimate = update_kalman_filter(sensor_positions_with_noise[i])
        kf_positions.append(kf_estimate)

    plt.plot(kf_positions[:i + 1], color='blue', alpha=0.5, label='Kalman Filter (KF) Estimate')

    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_linear + sensor_positions_with_noise),
             max(true_positions_linear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Linear One-Dimensional Motion with Kalman Filter (KF)')
    plt.legend()

# Main entry point
if __name__ == "__main__":
    # Create a figure and animation
    fig, ax = plt.subplots(figsize=(10, 6))
    ani = FuncAnimation(fig, animate_with_kalman, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

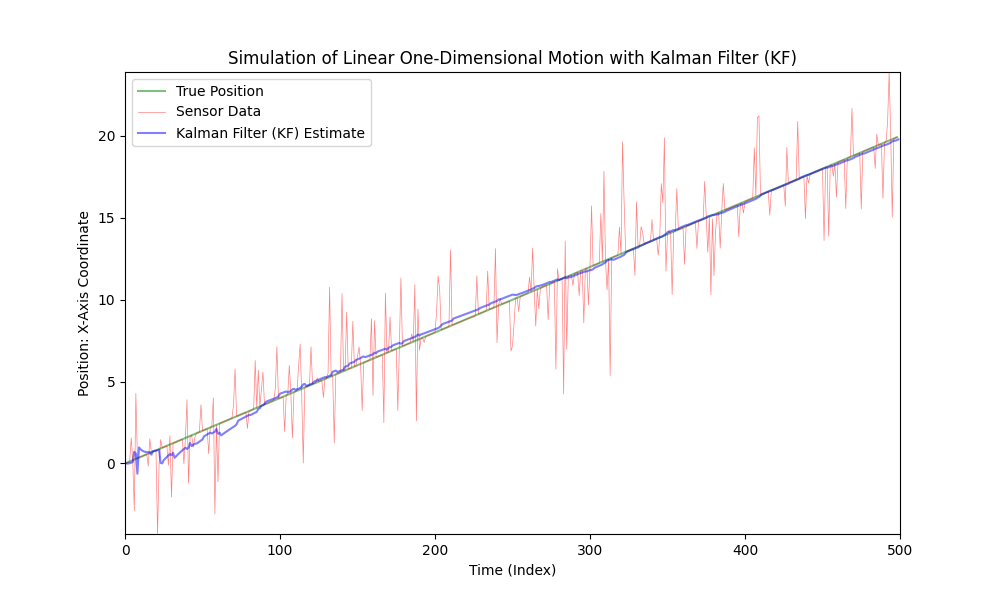
Wie gesehen, eignet sich der Kalman-Filter gut für den Einsatz in linearen Systemen, selbst bei starkem Rauschen. Die Bewegung des Autos ist jedoch nicht linear; das Auto beschleunigt mit unterschiedlichen Größen und Richtungen.

Lassen wir unseren Code etwas komplizierter werden, indem wir die Bewegung des Autos nichtlinear gestalten und eine variable Beschleunigung einführen. Zur Vereinfachung und Übersichtlichkeit verwenden wir eine sinusförmige Funktion, um die Beschleunigung zu modellieren. Wir werden den Geräuschpegel gleich halten.

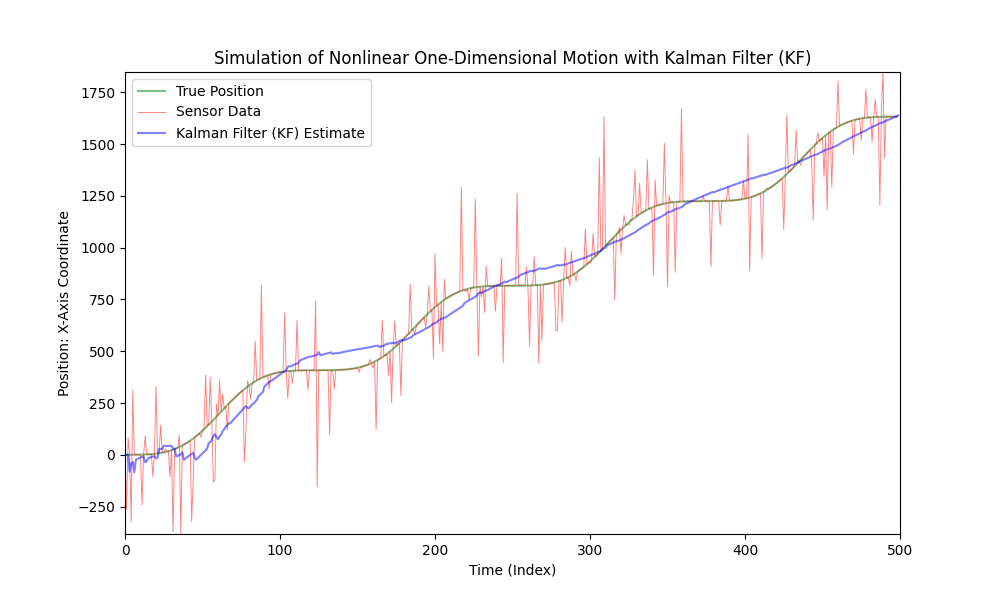
Wie wir sehen können, ist der klassische Kalman-Filter nicht für nichtlineare Modelle geeignet. Für diese Zwecke wurde der erweiterte Kalman-Filter (EKF) entwickelt.

Erweiterter Kalman-Filter (EKF)

Der Erweiterte Kalman-Filter (EKF) ist eine Modifikation des klassischen Kalman-Filters, der für die Arbeit mit nichtlinearen Systemen konzipiert ist. Während der Standard-Kalman-Filter für lineare Systeme vorgesehen ist, erweitert der EKF seine Anwendbarkeit, um nichtlineare Fälle zu behandeln.

Der erweiterte Kalman-Filter wurde nach dem ursprünglichen Kalman-Filter entwickelt, der 1960 von Rudolf Kalman eingeführt wurde. Er entstand als Ergebnis der Bemühungen von Ingenieuren und Wissenschaftlern, den Kalman-Filter für die Verwendung mit nichtlinearen Systemen anzupassen, insbesondere in den Bereichen Luft- und Raumfahrt sowie Schifffahrtsnavigation in den 1960er und 1970er Jahren. Das genaue Entstehungsdatum und die spezifischen Autoren sind weniger bekannt, da der EKF sich allmählich entwickelte und im Rahmen verschiedener Forschungsgruppen entstand.

Der erweiterte Kalman-Filter (EKF) wird häufig in Aufgaben verwendet, bei denen die Zustandsschätzung von Systemen, die durch nichtlineare Gleichungen beschrieben werden, erforderlich ist. Zu den Hauptanwendungsgebieten gehören die Robotik (zur Schätzung der Position und Orientierung von Robotern), die Automobilindustrie (in autonomen Fahrsystemen und Navigation), die Luft- und Raumfahrttechnik (für die orbitale Navigation von Satelliten und Raumfahrzeugen), die Mobilkommunikation und viele andere technische und ingenieurwissenschaftliche Felder.

Die wesentlichen Unterschiede zwischen dem erweiterten Kalman-Filter (EKF) und dem Standard-Kalman-Filter liegen hauptsächlich darin, wie sie die Dynamik und die Messungen des Systems handhaben.

Die wesentlichen Unterschiede umfassen Folgendes:

Umgang mit Nichtlinearität: Der Standard-Kalman-Filter nimmt an, dass die Systemdynamik und der Messprozess linear sind. Das bedeutet, dass die Zustandsübergangs- und Messfunktionen als lineare Matrizen dargestellt werden können. Der erweiterte Kalman-Filter (EKF) ist darauf ausgelegt, mit nichtlinearen Systemen zu arbeiten. Anstelle von linearen Matrizen verwendet er nichtlineare Funktionen, um die Systemdynamik und den Messprozess zu beschreiben.
Linearisierung: Im EKF wird die Linearisierung verwendet, um nichtlineare Funktionen anzunähern, typischerweise durch eine Taylorreihenentwicklung erster Ordnung um den aktuellen Zustandsschätzwert. Dies liefert linearisierte Gegenstücke der Zustandsübergangs- und Messfunktionen, die dann im Filter verwendet werden.
Zustandsübergangs- und Messfunktionen: Im Standard-Kalman-Filter werden die Zustandsübergangs- und Messfunktionen durch Matrizen dargestellt (z.B. Zustandsübergangsmatrix und Messmatrix). Im EKF können diese Funktionen beliebige differenzierbare nichtlineare Funktionen sein. Dies erhöht die Flexibilität, aber auch die Komplexität und die Anforderungen an die Rechenleistung.
Rechnerische Komplexität: Der EKF erfordert aufgrund der Notwendigkeit, nichtlineare Funktionen zu linearisieren und nachfolgende Berechnungen durchzuführen, eine höhere rechnerische Komplexität.

Der Hauptunterschied zwischen dem erweiterten Kalman-Filter und dem Standardfilter liegt in seiner Fähigkeit, mit nichtlinearen Systemen zu arbeiten, indem nichtlineare Funktionen und deren Linearisierung verwendet werden.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
import sys
import random

# Named constants
AMPLITUDE_FACTOR = 5.0  # Factor for amplitude in the nonlinear acceleration function
WAVES = 4  # Number of waves in the nonlinear motion model
INITIAL_POSITION = 0  # Initial position
TRUE_VELOCITY_INITIAL = 2.0  # Initial true velocity (changed to float)
TRUE_VELOCITY_INCREMENT = 0.2  # Increment for true velocity (added as a constant)
PREDICTION_INTERVAL = 10  # Interval for predictions
DIM_X = 2  # Dimension of state vector in Kalman filter
DIM_Z = 1  # Dimension of measurement vector in Kalman filter
INITIAL_P_COVARIANCE = 1000  # Initial state covariance for Kalman filter

# Initialize random number generator with the current time
random.seed()

# Read noise_percentage, noise_probability, and total_points from command line arguments
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = PREDICTION_INTERVAL / total_points  # Time interval between data points

# Define a nonlinear acceleration function that varies with time
def nonlinear_acceleration(t):
    # Calculate the amplitude of acceleration based on time
    amplitude = AMPLITUDE_FACTOR * 200.0 * (1 - abs((t % (total_points / WAVES) - (total_points / (2 * WAVES))) / (total_points / (2 * WAVES))))
    # Calculate the nonlinear acceleration based on time and amplitude
    return amplitude * np.sin(2.0 * np.pi * t / (total_points / WAVES))

# Function to add noise to true positions with a given probability
def add_noise(true_positions, probability):
    # Add Gaussian noise to true positions with specified probability
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions)) if random.uniform(0, 1) <= probability else p for p in true_positions]

# Function to update the Extended Kalman Filter (EKF) with sensor measurements
def update_extended_kalman_filter(z):
    ekf.predict()  # Predict the next state
    ekf.update(z)  # Update the state based on sensor measurements
    return ekf.x[0, 0]  # Return the estimated position

# Функция для закрытия анимации при нажатии клавиши ESC
def close_animation(event):
    if event.key == 'escape':
        plt.close()

# Function for creating an animation with EKF estimates
def animate_with_ekf(i):
    plt.cla()
    # Plot the true position and sensor data up to the current time
    plt.plot(true_positions_nonlinear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, label='Sensor Data', linewidth=0.5)

    if i < total_points:
        # Update the EKF with the current sensor measurement and obtain the estimate
        ekf_estimate = update_extended_kalman_filter(sensor_positions_with_noise[i])
        ekf_positions.append(ekf_estimate)

    # Plot the EKF estimate up to the current time
    plt.plot(ekf_positions[:i + 1], color='purple', alpha=0.5, label='Extended Kalman Filter (EKF) Estimate')

    # Set plot limits and labels
    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_nonlinear + sensor_positions_with_noise),
             max(true_positions_nonlinear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Nonlinear One-Dimensional Motion with Extended Kalman Filter (EKF)')
    plt.legend()

# Main entry point of the code
if __name__ == "__main__":
    # Create a figure for the animation
    fig, ax = plt.subplots(figsize=(10, 6))

    # Используйте connect для добавления обработчика событий
    fig.canvas.mpl_connect('key_press_event', close_animation)

    # Initialize true_positions_nonlinear with the initial position and true_velocity
    true_positions_nonlinear = [INITIAL_POSITION]
    true_velocity = TRUE_VELOCITY_INITIAL

    # Generate true positions based on the nonlinear motion model
    for t in range(1, total_points):
        acc = nonlinear_acceleration(t)
        true_velocity += acc * interval
        true_positions_nonlinear.append(true_positions_nonlinear[-1] + true_velocity * interval)

    # Add noise to true positions to simulate sensor data
    sensor_positions_with_noise = add_noise(true_positions_nonlinear, noise_probability)

    # Initialize an Extended Kalman Filter (EKF)
    ekf = KalmanFilter(dim_x=DIM_X, dim_z=DIM_Z)
    ekf.F = np.array([[1, interval],
                    [0, 1]])
    ekf.H = np.array([[1, 0]])
    ekf.P *= INITIAL_P_COVARIANCE
    ekf.R = noise_percentage * np.mean(true_positions_nonlinear)

    ekf_x = np.array([[sensor_positions_with_noise[0]],
                    [0]])
    ekf_positions = [ekf_x[0, 0]]

    # Create the animation using FuncAnimation
    ani = FuncAnimation(fig, animate_with_ekf, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

Wenden Sie den erweiterten Kalman-Filter für nichtlineare Bewegung an.

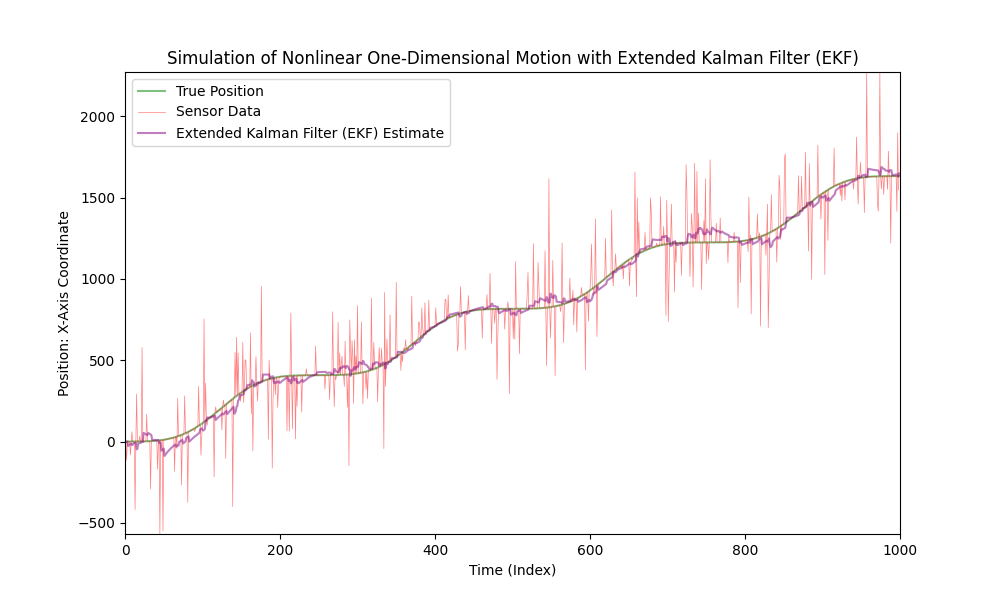
Nun, lassen wir das Niveau des Sensorsrauschens deutlich ansteigen.

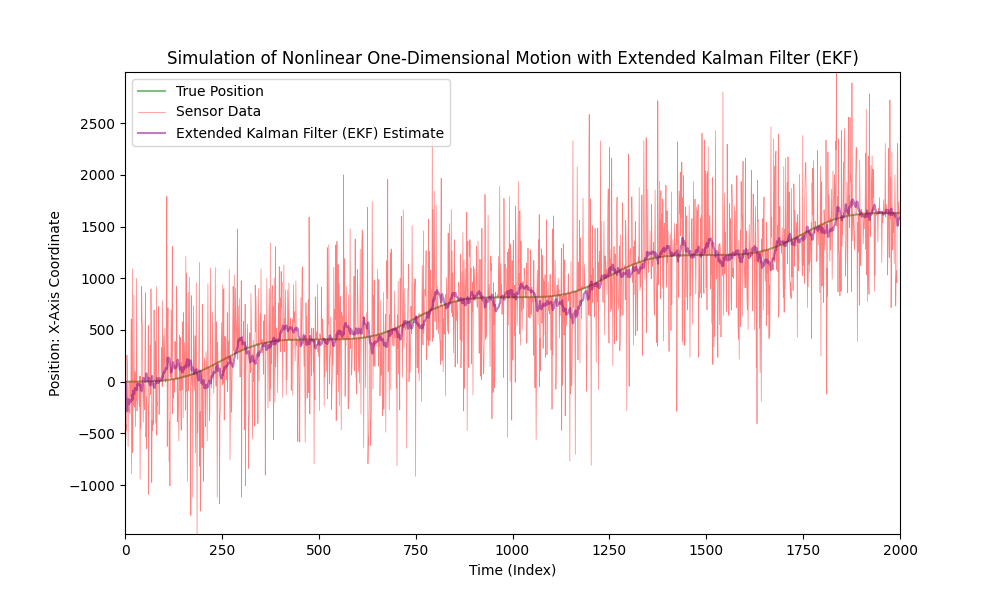
Wie wir sehen können, funktioniert der Extended Kalman Filter auch bei sehr verrauschten Daten gut.

Zusätzliche Materialien

https://en.wikipedia.org/wiki/Kalman_filter - Beschreibung des Filters und seiner grundlegenden mathematischen Funktionsprinzipien.

https://kalmanfilter.org/cpp/index.html - Beschreibung und Implementierung des Filters in C++.

https://commons.apache.org/proper/commons-math/javadocs/api-3.6.1/org/apache/commons/math3/filter/KalmanFilter.html - Beschreibung und Implementierung des Filters in Java.

https://filterpy.readthedocs.io/en/latest/kalman/KalmanFilter.html - Beschreibung und Implementierung des Filters in Python

Fazit

Der Extended Kalman Filter (EKF) ist ein leistungsfähiges Werkzeug zur Schätzung des Zustands dynamischer Systeme, insbesondere wenn diese Schätzung auf Daten von mehreren Sensoren gleichzeitig basieren muss. Ein wesentlicher Vorteil des EKF ist seine Fähigkeit, Informationen aus verschiedenen Quellen zu integrieren, was ihn in komplexen Systemen wie Fahrzeugnavigationssystemen, Robotik oder Luft- und Raumfahrttechnik außerordentlich nützlich macht.

Unter Berücksichtigung von lauten und oft unvollkommenen Daten verschiedener Sensoren ist das EKF in der Lage, diese Daten zu einem einheitlichen Ganzen zusammenzuführen und so eine genauere und zuverlässigere Zustandsschätzung zu liefern. Beispielsweise kann das EKF in einem Auto GPS-Daten verwenden, um die Position zu bestimmen, und Daten des Beschleunigungssensors, um Geschwindigkeit und Beschleunigung zu berechnen, und dadurch ein vollständigeres Bild der Bewegung des Fahrzeugs erstellen.

Der Extended Kalman Filter (EKF) ist in der Lage, die Gesamtunsicherheit, die durch das Rauschen und die Fehler jedes einzelnen Sensors entsteht, zu reduzieren. Da diese Fehler oft unkorreliert sind, ermöglicht ihre gemeinsame Verarbeitung im EKF stabilere und genauere Schätzungen. Es ist ebenfalls erwähnenswert, dass der EKF eine hohe Robustheit aufweist: Bei Problemen mit einem der Sensoren kann das System weiterhin funktionieren, indem es sich auf Daten der verbleibenden Sensoren stützt. Dies macht den EKF besonders wertvoll in kritischen Anwendungen, bei denen Zuverlässigkeit und Genauigkeit von höchster Wichtigkeit sind. Ein weiterer wichtiger Aspekt bei der Arbeit mit mehreren Sensoren ist die Zeitsynchronisation der Messungen. Der EKF bewältigt diese zeitlichen Unterschiede geschickt und gewährleistet eine korrekte Datenfusion.

Dank seiner Fähigkeit, Informationen aus mehreren Quellen zu aggregieren und zu analysieren, ist das EKF ein unschätzbares Werkzeug in Bereichen, in denen eine hohe Präzision der Zustandsschätzung unter Bedingungen der Unsicherheit und dynamischen Veränderungen erforderlich ist.

Zusammenfassend ist die Software zur Bekämpfung von Sensorrauschen ein anspruchsvoller Prozess, der statische, statistische Methoden und die Anwendung künstlicher Intelligenz zur Klassifizierung und Minderung von Rauscharten umfasst.

Unser Unternehmen besitzt umfangreiche Expertise im Umgang mit Problemen durch Sensorenlärm.

Bei Fragen zu diesem Artikel können Sie uns gerne kontaktieren unter articles@stofu.io.

Für Kooperationsmöglichkeiten können Sie uns über info@stofu.io. erreichen.

Alle Code-Dateien finden Sie in unserem Repository: https://github.com/SToFU-Systems/EKF_Usage.

Ich wünsche Ihnen alles Gute,

SToFU Systems Team

https://stofu.io

Softwareansatz zur Bewältigung von ADAS-Sensorgeräuschen (Teil 1)

Was ist ADAS?

Sensorrauschen in ADAS

Simulation der Punktverschiebung in einem eindimensionalen Koordinatensystem

Der Kalman-Filter

Erweiterter Kalman-Filter (EKF)

Zusätzliche Materialien

Fazit

Kategorien

Neueste Nachrichten

Softwareansatz zur Bewältigung von ADAS-Sensorgeräuschen (Teil 1)

PE-Ressourcenparser in C++ (Native)

Einführung in die Windows Kernel-Entwicklung mit Rust (Teil 1)

Einführung in die GPU-Programmierung

Innenansicht von BlackMatter: Technische Analyse der BlackMatter-Ransomware