Softwaretilgang til håndtering af støj fra ADAS-sensorer (Del 1)

Hvad er ADAS?

Moderne biler bliver mere og mere intelligente takket være ADAS (avancerede førerassistentsystemer), som forbedrer trafiksikkerheden og gør kørsel mere komfortabel. Disse systemer, der bruger kameraer, radarer og andre sensorer, hjælper med at styre køretøjet, detektere andre køretøjer, fodgængere og trafiklyssignaler, og giver føreren opdaterede oplysninger om vejforholdene og det omgivende miljø.

ADAS omfatter forskellige funktioner såsom adaptiv fartpilot, der justerer bilens hastighed til trafikken foran, vognbanehåndteringssystemer for at holde bilen i sin vognbane, automatisk bremsning for at forhindre kollisioner og automatiske parkeringssystemer for at lette parkeringsmanøvrer. Forskellige typer sensorer, såsom kameraer, radarer, lidarer og ultralydssensorer, sikrer disse systemers funktion, hvilket hjælper bilen med at tilpasse sig vejforhold og førerens kørestil.

Sensorstøj i ADAS

ADAS-sensorer, på trods af deres modernitet og kompleksitet, er tilbøjelige til støjforstyrrelser. Dette sker af flere årsager. For det første kan miljøet have uforudsigelige effekter på sensorerne. For eksempel kan snavs, støv, regn eller sne dække kameraer og radarer, hvilket forvrænger de informationer, de modtager. Det er som at forsøge at se igennem beskidt glas: ikke alt er synligt og ikke så klart, og udsynet er blokeret af mange artefakter. For det andet kan de tekniske begrænsninger i selve sensorerne også føre til støj. For eksempel kan sensorer fungere dårligt i svagt lys eller i stærke lyskontraster. Dette er ligesom at forsøge at skelne noget i mørket eller kigge på en alt for lys lyskilde – i begge tilfælde bliver det yderst vanskeligt at se detaljer. Når data, der modtages fra sensorer, er forvrængede, kan førerassistance-systemet misfortolke vej situationen, hvilket i visse situationer kan øge risikoen for trafikulykker.

Simulering af punktbevægelse i et eendimensionalt koordinatsystem

For at starte, lad os skrive koden til at simulere bevægelsen af en bil i et eendimensionalt rum. For at køre koden skal du opsætte et Python-miljø og installere de nødvendige biblioteker.

Her er trinene for at installere bibliotekerne og køre koden:

For at køre koden skal du opsætte et Python-miljø og installere de nødvendige biblioteker. Her er trinene til at installere bibliotekerne og køre koden: Installer Python: Hvis du ikke allerede har Python, kan du downloade og installere det fra den officielle Python-hjemmeside (https://www.python.org/downloads/). Det anbefales at bruge Python version 3.x.
Installer de nødvendige biblioteker: Åbn kommandolinjen (i Windows kan det være kommandoprompten eller PowerShell) og udfør følgende kommando for at installere bibliotekerne:
```
pip install matplotlib numpy filterpy
```
Gem din kode: Kopier den kode, du har givet, og gem den i en fil med udvidelsen .py (for eksempel simulation.py)
Kør koden: I kommandolinjen, naviger til mappen, hvor din kodefil er placeret, og eksekver den med følgende kommando:
```
python simulation.py 20 20 500
```
Denne kommando vil køre koden med argumenter 20 (for støj amplitude), 20 (for støj frekvens), og 500 (for det samlede antal datapunkter på grafen). Du kan ændre argumentværdierne efter behov.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
import sys
import random
import time

# Named constants
AMPLITUDE_FACTOR = 5.0  # Factor for amplitude in the nonlinear acceleration function
WAVES = 4  # Number of waves in the nonlinear motion model
INITIAL_POSITION = 0  # Initial position
TRUE_VELOCITY_INITIAL = 2.0  # Initial true velocity (changed to float)
TRUE_VELOCITY_INCREMENT = 0.2  # Increment for true velocity (added as a constant)
PREDICTION_INTERVAL = 10  # Interval for predictions
DIM_X = 2  # Dimension of state vector in Kalman filter
DIM_Z = 1  # Dimension of measurement vector in Kalman filter
INITIAL_P_COVARIANCE = 1000  # Initial state covariance for Kalman filter
RANDOM_SEED = 42  # Seed for random number generator

# Initialize random number generator with the current time
random.seed(int(time.time()))  # Using the current time to initialize the random number generator

# Read noise_percentage, noise_probability, and total_points from command line arguments
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = PREDICTION_INTERVAL / total_points  # Time interval between data points

# Define a nonlinear acceleration function that varies with time
def nonlinear_acceleration(t):
    # Calculate the amplitude of acceleration based on time
    amplitude = AMPLITUDE_FACTOR * 200.0 * (1 - abs((t % (total_points / WAVES) - (total_points / (2 * WAVES))) / (total_points / (2 * WAVES))))
    # Calculate the nonlinear acceleration based on time and amplitude
    return amplitude * np.sin(2.0 * np.pi * t / (total_points / WAVES))

# Function to add noise to true positions with a given probability
def add_noise(true_positions, probability):
    # Add Gaussian noise to true positions with specified probability
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions)) if random.uniform(0, 1) <= probability else p for p in true_positions]

# Function to close the animation on pressing the ESC key
def close_animation(event):
    if event.key == 'escape':
        plt.close()

# Function for creating an animation without the Kalman Filter
def animate_without_ekf(i):
    plt.cla()
    # Plot the true position and sensor data up to the current time
    plt.plot(true_positions_nonlinear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, label='Sensor Data', linewidth=0.5)

    # Set plot limits and labels
    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_nonlinear + sensor_positions_with_noise),
             max(true_positions_nonlinear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Nonlinear One-Dimensional Motion')

    # Display the legend
    plt.legend()

# Main entry point of the code
if __name__ == "__main__":
    # Create a figure for the animation
    fig, ax = plt.subplots(figsize=(10, 6))

    # Use connect to add an event handler for key presses
    fig.canvas.mpl_connect('key_press_event', close_animation)

    # Initialize true_positions_nonlinear with the initial position and true_velocity
    true_positions_nonlinear = [INITIAL_POSITION]
    true_velocity = TRUE_VELOCITY_INITIAL

    # Generate true positions based on the nonlinear motion model
    for t in range(1, total_points):
        acc = nonlinear_acceleration(t)
        true_velocity += acc * interval
        true_positions_nonlinear.append(true_positions_nonlinear[-1] + true_velocity * interval)

    # Add noise to true positions to simulate sensor data
    sensor_positions_with_noise = add_noise(true_positions_nonlinear, noise_probability)

    # Create the animation using FuncAnimation
    ani = FuncAnimation(fig, animate_without_ekf, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

Dette er en simulering af en bils bevægelse i eendimensionalt rum:

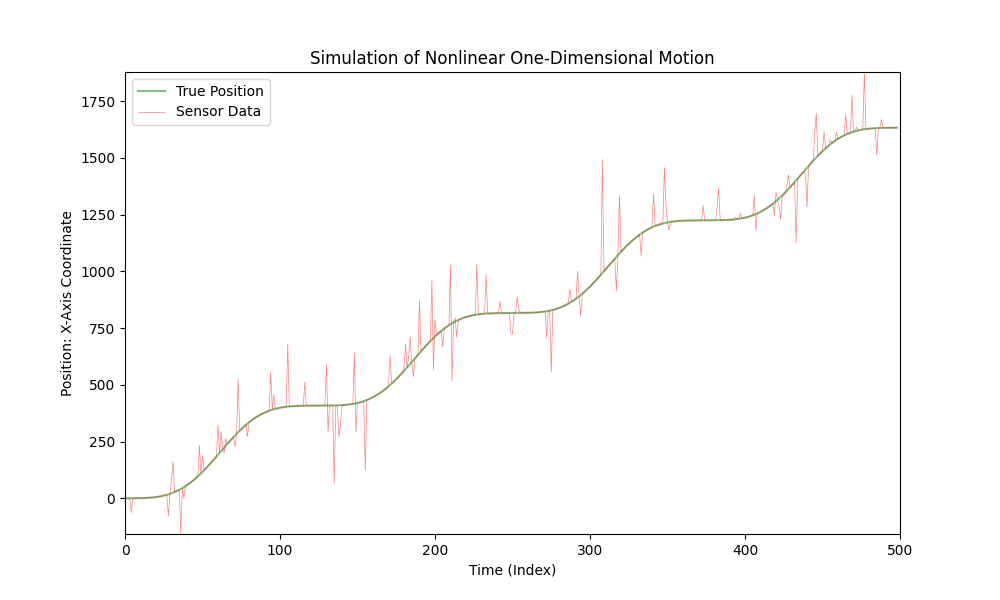
Bilen bevæger sig med varierende acceleration, og en sensor måler bilens X-koordinat. I denne simulation tilføjer vi støj til sensordataene for at tage højde for mulige målefejl.

Koden, der blev leveret tidligere, visualiserer denne simulation, hvor den grønne linje repræsenterer bilens "sande" position, og den røde linje repræsenterer sensordataene, under hensyntagen til den tilføjede støj. Accelerationen ændres over tid, hvilket skaber en mere realistisk simulation af bilens bevægelse.

Denne kode kan bruges til at visualisere og analysere forskellige scenarier af bilbevægelse under hensyntagen til skiftende acceleration og mulige sensorfejl.

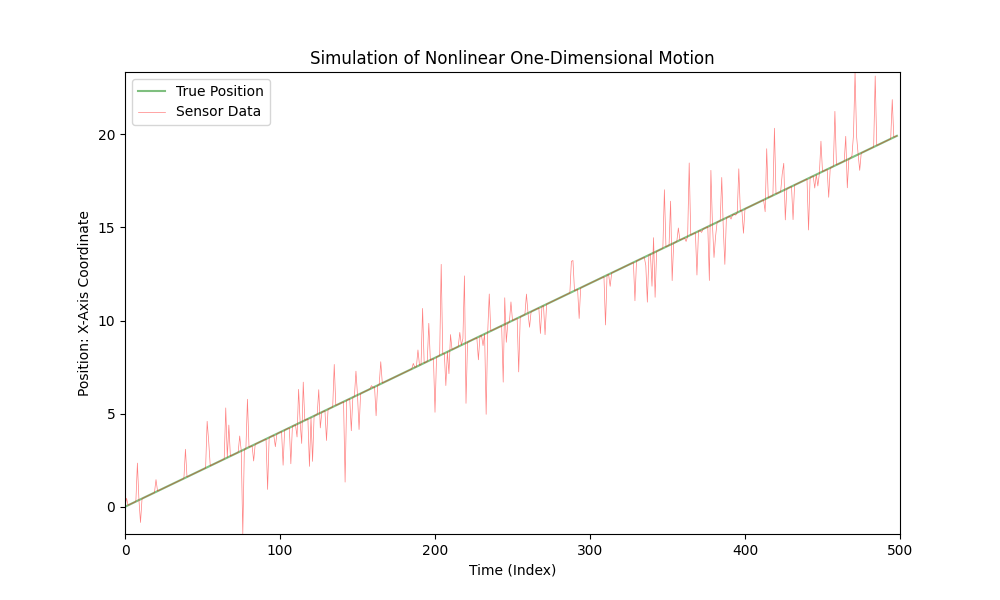
For at simulere lineær bevægelse, kan du blot ændre nonlinear_acceleration(t) funktionen til altid at returnere 0:

def nonlinear_acceleration(t):
    return 0

Denne ændring vil gøre bilens bevægelse lineær med konstant hastighed.

Kalman-filtret

Kalman-filteret er en algoritme udviklet af Rudolf E. Kalman i 1960. Denne algoritme gør det muligt at estimere tilstanden af et dynamisk system baseret på et sæt ufuldstændige og støjfyldte målinger. Oprindeligt blev Kalman-filteret udviklet til at løse problemer inden for rumfartsteknik, men med tiden har det fundet bred anvendelse i forskellige felter. Den største fordel ved Kalman-filteret er, at det er rekursivt, hvilket betyder, at det bruger de seneste målinger og den forrige tilstand til at beregne systemets aktuelle tilstand. Dette gør det effektivt til online realtidsdataforarbejdning.

Kalman-filteret har fundet anvendelse i mange områder, herunder navigation og køretøjskontrol, signalbehandling, økonometri, robotteknik, og mange andre områder, hvor estimering af tidsvarierende processer baseret på uperfekte eller ufuldstændige data er nødvendigt.

Kalman-filteret har flere nøglefordele sammenlignet med andre algoritmer til skøn og filtrering af data:

Optimalitet: Under visse betingelser (lineært system, gaussisk støj) er Kalman-filteret optimalt med hensyn til at minimere middelkvadratisk estimeringsfejl.
Effektivitet i realtid: Kalman-filteret er rekursivt, hvilket betyder, at det kun bruger de seneste målinger og den forrige tilstand til at beregne den nuværende tilstand. Dette gør det velegnet til realtidsapplikationer.
Minimalt hukommelseskrav: Eftersom filteret kun bruger den seneste måling og den aktuelle tilstandsestimering, behøver det ikke at gemme hele datahistorikken.
Robusthed over for målefejl: Filteret er i stand til effektivt at behandle støjfyldte data, hvilket minimerer indvirkningen af tilfældige målefejl.
Versatile anvendelser: På grund af sin alsidighed er Kalman-filteret blevet anvendt i forskellige felter, fra rumfartsteknik til økonometri.
Let at implementere: Algoritmen er forholdsvis let at forstå og implementere, hvilket gør den tilgængelig for et bredt udvalg af fagfolk.

Lad os implementere et grundlæggende Kalman-filter til en sensor, der måler positionen af vores bil, som bevæger sig i et eendimensionalt system med konstant hastighed, men med støjende sensoraflæsninger.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
import sys
import random

# Read noise_percentage, noise_probability, total_points from the command line
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = 10 / total_points

# Initialize true positions and velocity
true_positions_linear = [0]
true_velocity = 2

for t in range(1, total_points):
    true_positions_linear.append(true_positions_linear[-1] + true_velocity * interval)

# Function to add noise to true positions
def add_noise(true_positions, probability):
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions))
            if random.uniform(0, 1) <= probability else p for p in true_positions]

sensor_positions_with_noise = add_noise(true_positions_linear, noise_probability)

# Initialize Kalman Filter (KF)
kf = KalmanFilter(dim_x=2, dim_z=1)
kf.F = np.array([[1, interval],
                 [0, 1]])
kf.H = np.array([[1, 0]])
kf.P *= 1000
kf.R = noise_percentage * np.mean(true_positions_linear)
kf.Q = Q_discrete_white_noise(dim=2, dt=interval, var=0.001)

x = np.array([[sensor_positions_with_noise[0]],
              [0]])
kf_positions = [x[0, 0]]

# Function to update Kalman Filter with sensor data
def update_kalman_filter(z):
    kf.predict()
    kf.update(z)
    return kf.x[0, 0]

# Function to create an animation with Kalman Filter (KF) estimation
def animate_with_kalman(i):
    plt.cla()
    plt.plot(true_positions_linear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, linewidth=0.5, label='Sensor Data')

    if i < total_points:
        kf_estimate = update_kalman_filter(sensor_positions_with_noise[i])
        kf_positions.append(kf_estimate)

    plt.plot(kf_positions[:i + 1], color='blue', alpha=0.5, label='Kalman Filter (KF) Estimate')

    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_linear + sensor_positions_with_noise),
             max(true_positions_linear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Linear One-Dimensional Motion with Kalman Filter (KF)')
    plt.legend()

# Main entry point
if __name__ == "__main__":
    # Create a figure and animation
    fig, ax = plt.subplots(figsize=(10, 6))
    ani = FuncAnimation(fig, animate_with_kalman, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

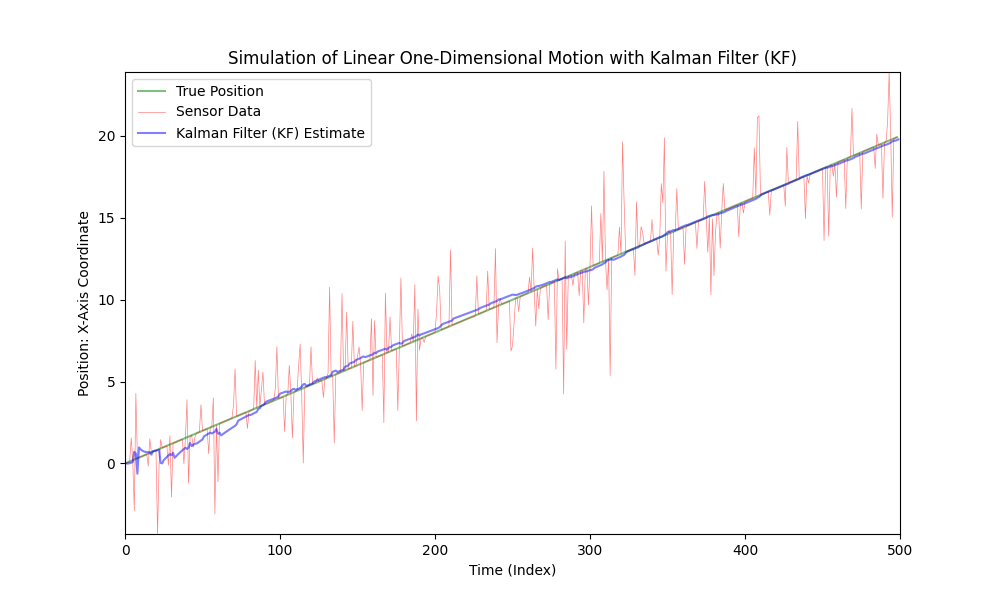
Som set er Kalman-filteret velegnet til brug i lineære systemer selv med kraftig støj. Dog er bilens bevægelse ikke lineær; bilen accelererer med varierende størrelser og retninger.

Lad os komplicere vores kode en smule ved at gøre bilens bevægelse ikke-lineær og ved at indføre variabel acceleration. For enkelhedens og klarhedens skyld vil vi bruge en sinusfunktion til at modellere accelerationen. Vi vil holde støjniveauet det samme.

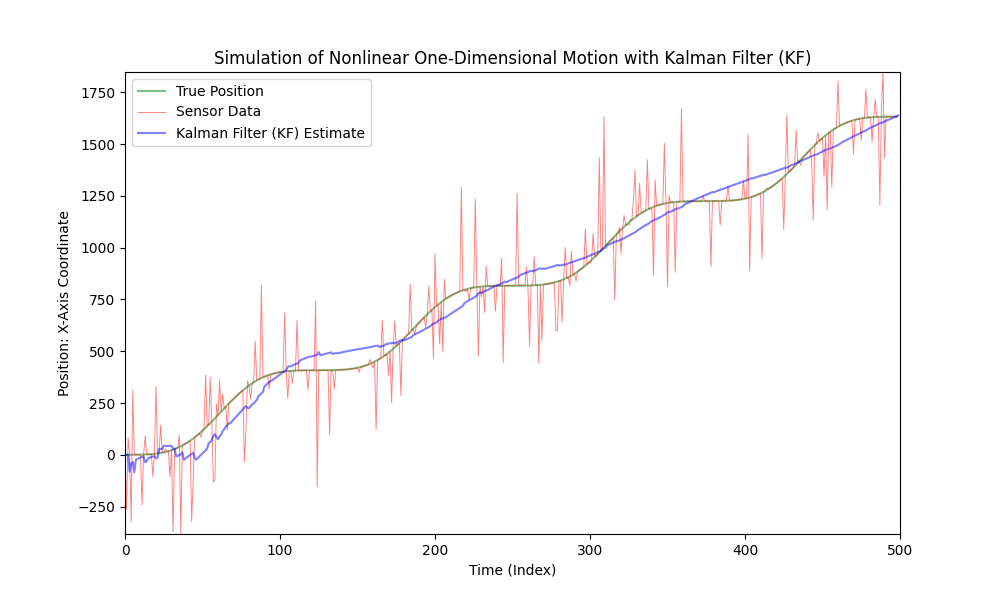
Som vi kan se, er den klassiske Kalman-filter ikke egnet til ikke-lineære modeller. Til disse formål blev den Udvidede Kalman-filter (EKF) udviklet.

Udvidet Kalman-filter (EKF)

Den Udvidede Kalman Filter (EKF) er en modifikation af den klassiske Kalman Filter designet til at arbejde med ikke-lineære systemer. Mens den standard Kalman Filter er beregnet til lineære systemer, udvider EKF dens anvendelighed til at håndtere ikke-lineære tilfælde.

Den udvidede Kalman-filter blev udviklet efter det oprindelige Kalman-filter, introduceret af Rudolf Kalman i 1960. Det opstod som et resultat af bestræbelser fra ingeniører og videnskabsfolk på at tilpasse Kalman-filteret til brug med ikke-lineære systemer, især inden for luftfarts- og marine navigationsområderne i 1960'erne og 1970'erne. Den præcise dato for dets oprettelse og specifikke forfattere er mindre velkendte, da EKF udviklede sig gradvist og inden for rammerne af forskellige forskningsgrupper.

Den udvidede Kalman-filter (EKF) bruges bredt i opgaver hvor tilstandsestimering af systemer beskrevet af ikke-lineære ligninger er nødvendig. Dets primære anvendelsesområder inkluderer robotteknik (til estimering af position og orientering af robotter), bilindustrien (i autonome køresystemer og navigation), rumfartsteknik (til satellitbanenavigation og rumfartøjer), mobilkommunikation og mange andre tekniske og ingeniørmæssige felter.

De væsentlige forskelle mellem Extended Kalman Filter (EKF) og det standard Kalman Filter ligger primært i, hvordan de håndterer systemets dynamik og målinger.

De primære forskelle inkluderer følgende:

Håndtering af ikke-linearitet: Den standard Kalman-filter antager, at systemdynamikker og måleprocesser er lineære. Dette betyder, at tilstandsovergangs- og målefunktionerne kan repræsenteres som lineære matricer. Det udvidede Kalman-filter (EKF) er designet til at arbejde med ikke-lineære systemer. I stedet for lineære matricer bruger det ikke-lineære funktioner til at beskrive systemdynamikker og måleprocesser.
Linearisering: I EKF bruges linearisering til at tilnærme ikke-lineære funktioner, typisk gennem en førsteordens Taylor-serieudvidelse omkring den nuværende tilstands-vurdering. Dette tilvejebringer lineariserede modstykker til tilstandsovergangs- og målefunktionerne, som derefter bruges i filteret.
Tilstandsovergangs- og målefunktioner: I den standard Kalman-filter repræsenteres tilstandsovergangs- og målefunktionerne af matricer (f.eks. tilstandsovergangsmatrice og målematrice). I EKF kan disse funktioner være hvilken som helst differentierbar ikke-lineær funktion. Dette tilføjer fleksibilitet, men også øger kompleksitet og beregningskrav.
Beregningens kompleksitet: EKF kræver højere beregningskompleksitet på grund af behovet for at linearisere ikke-lineære funktioner og efterfølgende beregninger.

Hovedforskellen mellem den udvidede Kalman-filter og den standard er dens evne til at arbejde med ikke-lineære systemer ved brug af ikke-lineære funktioner og deres linearisering.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
import sys
import random

# Named constants
AMPLITUDE_FACTOR = 5.0  # Factor for amplitude in the nonlinear acceleration function
WAVES = 4  # Number of waves in the nonlinear motion model
INITIAL_POSITION = 0  # Initial position
TRUE_VELOCITY_INITIAL = 2.0  # Initial true velocity (changed to float)
TRUE_VELOCITY_INCREMENT = 0.2  # Increment for true velocity (added as a constant)
PREDICTION_INTERVAL = 10  # Interval for predictions
DIM_X = 2  # Dimension of state vector in Kalman filter
DIM_Z = 1  # Dimension of measurement vector in Kalman filter
INITIAL_P_COVARIANCE = 1000  # Initial state covariance for Kalman filter

# Initialize random number generator with the current time
random.seed()

# Read noise_percentage, noise_probability, and total_points from command line arguments
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = PREDICTION_INTERVAL / total_points  # Time interval between data points

# Define a nonlinear acceleration function that varies with time
def nonlinear_acceleration(t):
    # Calculate the amplitude of acceleration based on time
    amplitude = AMPLITUDE_FACTOR * 200.0 * (1 - abs((t % (total_points / WAVES) - (total_points / (2 * WAVES))) / (total_points / (2 * WAVES))))
    # Calculate the nonlinear acceleration based on time and amplitude
    return amplitude * np.sin(2.0 * np.pi * t / (total_points / WAVES))

# Function to add noise to true positions with a given probability
def add_noise(true_positions, probability):
    # Add Gaussian noise to true positions with specified probability
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions)) if random.uniform(0, 1) <= probability else p for p in true_positions]

# Function to update the Extended Kalman Filter (EKF) with sensor measurements
def update_extended_kalman_filter(z):
    ekf.predict()  # Predict the next state
    ekf.update(z)  # Update the state based on sensor measurements
    return ekf.x[0, 0]  # Return the estimated position

# Функция для закрытия анимации при нажатии клавиши ESC
def close_animation(event):
    if event.key == 'escape':
        plt.close()

# Function for creating an animation with EKF estimates
def animate_with_ekf(i):
    plt.cla()
    # Plot the true position and sensor data up to the current time
    plt.plot(true_positions_nonlinear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, label='Sensor Data', linewidth=0.5)

    if i < total_points:
        # Update the EKF with the current sensor measurement and obtain the estimate
        ekf_estimate = update_extended_kalman_filter(sensor_positions_with_noise[i])
        ekf_positions.append(ekf_estimate)

    # Plot the EKF estimate up to the current time
    plt.plot(ekf_positions[:i + 1], color='purple', alpha=0.5, label='Extended Kalman Filter (EKF) Estimate')

    # Set plot limits and labels
    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_nonlinear + sensor_positions_with_noise),
             max(true_positions_nonlinear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Nonlinear One-Dimensional Motion with Extended Kalman Filter (EKF)')
    plt.legend()

# Main entry point of the code
if __name__ == "__main__":
    # Create a figure for the animation
    fig, ax = plt.subplots(figsize=(10, 6))

    # Используйте connect для добавления обработчика событий
    fig.canvas.mpl_connect('key_press_event', close_animation)

    # Initialize true_positions_nonlinear with the initial position and true_velocity
    true_positions_nonlinear = [INITIAL_POSITION]
    true_velocity = TRUE_VELOCITY_INITIAL

    # Generate true positions based on the nonlinear motion model
    for t in range(1, total_points):
        acc = nonlinear_acceleration(t)
        true_velocity += acc * interval
        true_positions_nonlinear.append(true_positions_nonlinear[-1] + true_velocity * interval)

    # Add noise to true positions to simulate sensor data
    sensor_positions_with_noise = add_noise(true_positions_nonlinear, noise_probability)

    # Initialize an Extended Kalman Filter (EKF)
    ekf = KalmanFilter(dim_x=DIM_X, dim_z=DIM_Z)
    ekf.F = np.array([[1, interval],
                    [0, 1]])
    ekf.H = np.array([[1, 0]])
    ekf.P *= INITIAL_P_COVARIANCE
    ekf.R = noise_percentage * np.mean(true_positions_nonlinear)

    ekf_x = np.array([[sensor_positions_with_noise[0]],
                    [0]])
    ekf_positions = [ekf_x[0, 0]]

    # Create the animation using FuncAnimation
    ani = FuncAnimation(fig, animate_with_ekf, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

Anvend den udvidede Kalman-filter til ikke-lineær bevægelse.

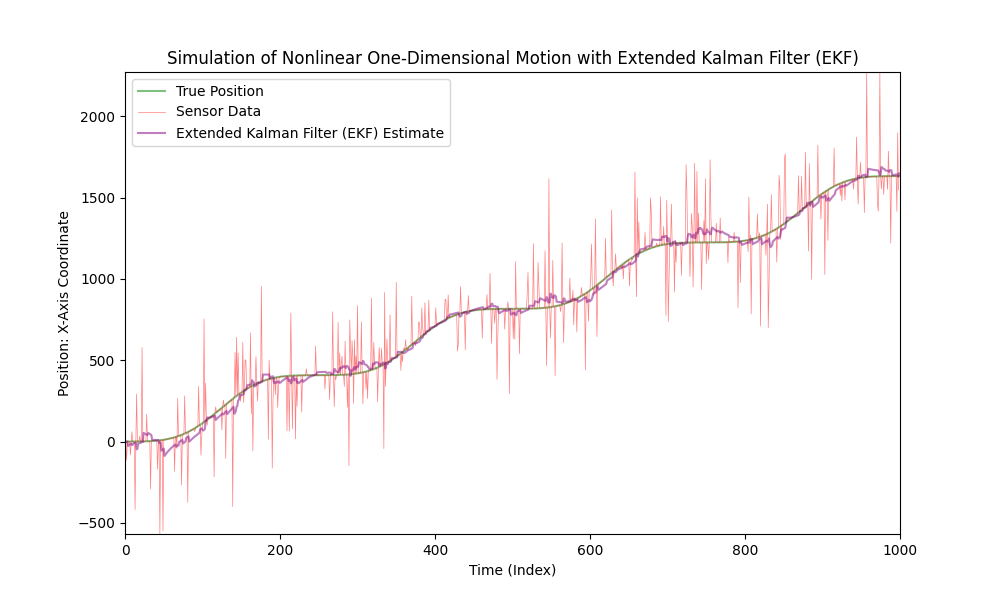
Nu, lad os markant øge niveauet af sensorstøj.

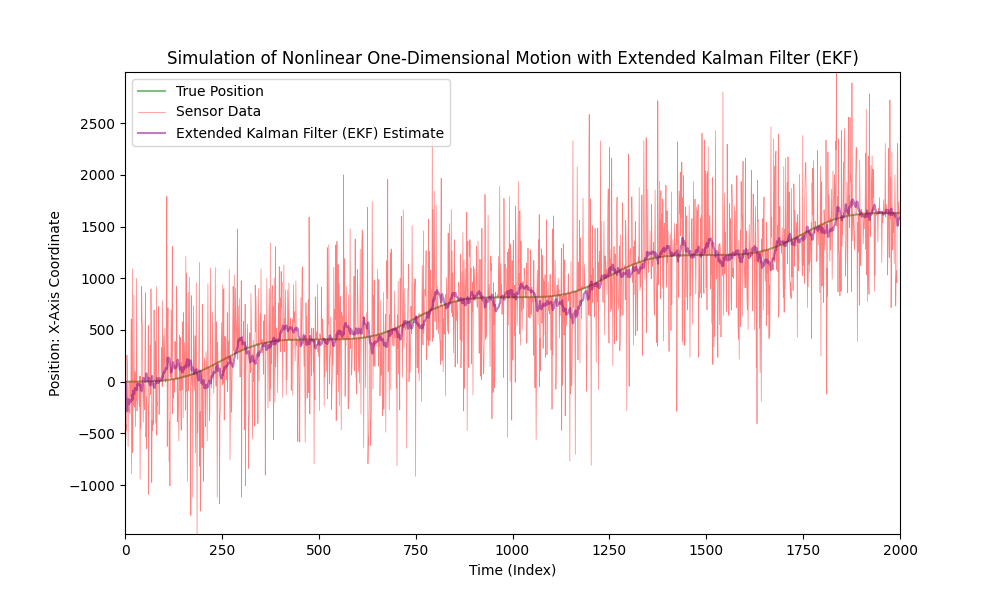
Som vi kan se, fungerer den udvidede Kalman-filter godt selv i tilfælde af meget støjende data.

Yderligere materialer

https://en.wikipedia.org/wiki/Kalman_filter - Beskrivelse af filteret og dets grundlæggende matematiske driftsprincipper.

https://kalmanfilter.org/cpp/index.html - Beskrivelse og implementering af filteret i C++.

https://commons.apache.org/proper/commons-math/javadocs/api-3.6.1/org/apache/commons/math3/filter/KalmanFilter.html - Beskrivelse og implementering af filteret i Java.

https://filterpy.readthedocs.io/en/latest/kalman/KalmanFilter.html - Beskrivelse og implementering af filteret i Python

Afslutning

Den udvidede Kalman-filter (EKF) er et kraftfuldt værktøj til estimering af tilstanden af dynamiske systemer, især når denne estimering skal baseres på data fra flere sensorer samtidigt. En af de væsentlige fordele ved EKF er dens evne til at integrere information fra forskellige kilder, hvilket gør den exceptionelt nyttig i komplekse systemer såsom bilnavigationssystemer, robotteknik eller rumfartsteknik.

Under hensyntagen til støjende og ofte uperfekte data fra forskellige sensorer er EKF i stand til at sammenflette disse data til en samlet helhed, hvilket giver et mere præcist og pålideligt tilstandsestimat. For eksempel kan EKF i en bil bruge GPS-data til at bestemme position og accelerometredata til at beregne hastighed og acceleration, og dermed skabe et mere fuldstændigt billede af køretøjets bevægelse.

Den Udvidede Kalman Filter (EKF) er i stand til at reducere den samlede usikkerhed, der opstår på grund af støj og fejl fra hver enkelt sensor. Da disse fejl ofte er ukorrelerede, muliggør deres fælles behandling i EKF mere stabile og nøjagtige estimater. Det er også værd at bemærke, at EKF udviser høj robusthed: i tilfælde af problemer med en af sensorerne, kan systemet fortsætte med at fungere ved at stole på data fra de resterende. Dette gør EKF særligt værdifuld i kritiske applikationer, hvor pålidelighed og nøjagtighed er af største betydning. Et andet vigtigt aspekt, når man arbejder med flere sensorer, er tidssynkronisering af målinger. EKF håndterer dygtigt disse tidsmæssige forskelle og sikrer korrekt datafusion.

Takket være dens evne til at aggregere og analysere information fra flere kilder, er EKF et uvurderligt værktøj i områder, hvor der kræves høj præcisionsstatsestimering under betingelser med usikkerhed og dynamiske ændringer.

I konklusion er software til bekæmpelse af sensorstøj en udfordrende proces, der omfatter statiske, statistiske metoder samt anvendelsen af kunstig intelligens til klassificering og afhjælpning af støjtyper.

Vores firma besidder betydelig ekspertise i håndtering af problemer med sensorstøj.

For henvendelser vedrørende denne artikel, er du velkommen til at kontakte os på articles@stofu.io.

For samarbejdsmuligheder kan du kontakte os på info@stofu.io.

Alle kodefiler kan du finde i vores repository: https://github.com/SToFU-Systems/EKF_Usage.

Ønsker dig alt det bedste,

SToFU Systems Team

https://stofu.io

Softwaretilgang til håndtering af støj fra ADAS-sensorer (Del 1)

Hvad er ADAS?

Sensorstøj i ADAS

Simulering af punktbevægelse i et eendimensionalt koordinatsystem

Kalman-filtret

Udvidet Kalman-filter (EKF)

Yderligere materialer

Afslutning

Categorieën

Recent nieuws

Softwaretilgang til håndtering af støj fra ADAS-sensorer (Del 1)

PE Resource Parser i C++ (Native)

Introduktion til Windows Kerneludvikling i Rust (Del 1)

Introduktion til GPU-programmering

Inde i BlackMatter: Teknisk analyse af BlackMatter ransomware