Enfoque de software para tratar el ruido de los sensores ADAS (Parte 1)

¿Qué es ADAS?

Los automóviles modernos se están volviendo cada vez más inteligentes gracias a los sistemas ADAS (Sistemas Avanzados de Asistencia al Conductor) que mejoran la seguridad vial y hacen que la conducción sea más cómoda. Estos sistemas, utilizando cámaras, radares y otros sensores, ayudan en el control del vehículo, detectan otros vehículos, peatones y señales de semáforos, proporcionando al conductor información actualizada sobre las condiciones de la carretera y el entorno circundante.

ADAS incluye diversas funciones como el control de crucero adaptativo, que ajusta la velocidad del automóvil al tráfico delantero, sistemas de gestión de carriles para mantener el coche en su carril, frenado automático para prevenir colisiones y sistemas de estacionamiento automático para facilitar las maniobras de aparcamiento. Diferentes tipos de sensores, como cámaras, radares, lidars y sensores ultrasónicos, aseguran el funcionamiento de estos sistemas, ayudando al automóvil a adaptarse a las condiciones de la carretera y al estilo de conducción del conductor.

Ruido del Sensor en ADAS

Los sensores ADAS, a pesar de su modernidad y complejidad, son propensos a interferencias de ruido. Esto ocurre por varias razones. En primer lugar, el entorno puede tener efectos impredecibles sobre los sensores. Por ejemplo, la suciedad, el polvo, la lluvia o la nieve pueden cubrir cámaras y radares, distorsionando la información que reciben. Es como tratar de mirar a través de un vidrio sucio: no todo es visible y no tan claro, y la vista está obstruida por muchos artefactos. En segundo lugar, las limitaciones técnicas de los propios sensores también pueden llevar a ruido. Por ejemplo, los sensores pueden funcionar mal en condiciones de poca luz o en fuertes contrastes de luz. Esto es similar a tratar de discernir algo en la oscuridad o mirar una fuente de luz excesivamente brillante. En ambos casos, se vuelve extremadamente difícil ver detalles. Cuando los datos recibidos de los sensores están distorsionados, el sistema de asistencia al conductor puede interpretar mal la situación de la carretera, lo que en ciertas situaciones puede aumentar el riesgo de accidentes de tráfico.

Simulación del Movimiento de un Punto en un Sistema de Coordenadas Unidimensional

Para comenzar, escribamos el código para simular el movimiento de un automóvil en un espacio unidimensional. Para ejecutar el código, necesitarás configurar un entorno de Python e instalar las librerías necesarias.

Aquí están los pasos para instalar las bibliotecas y ejecutar el código:

Para ejecutar el código, necesitarás configurar un entorno de Python e instalar las librerías necesarias. Aquí están los pasos para instalar las librerías y ejecutar el código: Instalar Python: Si aún no tienes Python, descárgalo e instálalo desde el sitio web oficial de Python (https://www.python.org/downloads/). Se recomienda usar la versión de Python 3.x.
Instalar las librerías necesarias: Abre la línea de comandos (en Windows podría ser el símbolo del sistema o PowerShell) y ejecuta el siguiente comando para instalar las librerías:
```
pip install matplotlib numpy filterpy
```
Guarda tu código: Copia el código que proporcionaste y guárdalo en un archivo con la extensión .py (por ejemplo, simulation.py)
Ejecuta el código: En la línea de comandos, navega hasta el directorio donde se encuentra tu archivo de código y ejecútalo con el siguiente comando:
```
python simulation.py 20 20 500
```
Este comando ejecutará el código con los argumentos 20 (para la amplitud del ruido), 20 (para la frecuencia del ruido), y 500 (para el total de puntos de datos en el gráfico). Puedes cambiar los valores de los argumentos según sea necesario.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
import sys
import random
import time

# Named constants
AMPLITUDE_FACTOR = 5.0  # Factor for amplitude in the nonlinear acceleration function
WAVES = 4  # Number of waves in the nonlinear motion model
INITIAL_POSITION = 0  # Initial position
TRUE_VELOCITY_INITIAL = 2.0  # Initial true velocity (changed to float)
TRUE_VELOCITY_INCREMENT = 0.2  # Increment for true velocity (added as a constant)
PREDICTION_INTERVAL = 10  # Interval for predictions
DIM_X = 2  # Dimension of state vector in Kalman filter
DIM_Z = 1  # Dimension of measurement vector in Kalman filter
INITIAL_P_COVARIANCE = 1000  # Initial state covariance for Kalman filter
RANDOM_SEED = 42  # Seed for random number generator

# Initialize random number generator with the current time
random.seed(int(time.time()))  # Using the current time to initialize the random number generator

# Read noise_percentage, noise_probability, and total_points from command line arguments
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = PREDICTION_INTERVAL / total_points  # Time interval between data points

# Define a nonlinear acceleration function that varies with time
def nonlinear_acceleration(t):
    # Calculate the amplitude of acceleration based on time
    amplitude = AMPLITUDE_FACTOR * 200.0 * (1 - abs((t % (total_points / WAVES) - (total_points / (2 * WAVES))) / (total_points / (2 * WAVES))))
    # Calculate the nonlinear acceleration based on time and amplitude
    return amplitude * np.sin(2.0 * np.pi * t / (total_points / WAVES))

# Function to add noise to true positions with a given probability
def add_noise(true_positions, probability):
    # Add Gaussian noise to true positions with specified probability
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions)) if random.uniform(0, 1) <= probability else p for p in true_positions]

# Function to close the animation on pressing the ESC key
def close_animation(event):
    if event.key == 'escape':
        plt.close()

# Function for creating an animation without the Kalman Filter
def animate_without_ekf(i):
    plt.cla()
    # Plot the true position and sensor data up to the current time
    plt.plot(true_positions_nonlinear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, label='Sensor Data', linewidth=0.5)

    # Set plot limits and labels
    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_nonlinear + sensor_positions_with_noise),
             max(true_positions_nonlinear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Nonlinear One-Dimensional Motion')

    # Display the legend
    plt.legend()

# Main entry point of the code
if __name__ == "__main__":
    # Create a figure for the animation
    fig, ax = plt.subplots(figsize=(10, 6))

    # Use connect to add an event handler for key presses
    fig.canvas.mpl_connect('key_press_event', close_animation)

    # Initialize true_positions_nonlinear with the initial position and true_velocity
    true_positions_nonlinear = [INITIAL_POSITION]
    true_velocity = TRUE_VELOCITY_INITIAL

    # Generate true positions based on the nonlinear motion model
    for t in range(1, total_points):
        acc = nonlinear_acceleration(t)
        true_velocity += acc * interval
        true_positions_nonlinear.append(true_positions_nonlinear[-1] + true_velocity * interval)

    # Add noise to true positions to simulate sensor data
    sensor_positions_with_noise = add_noise(true_positions_nonlinear, noise_probability)

    # Create the animation using FuncAnimation
    ani = FuncAnimation(fig, animate_without_ekf, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

Esta es una simulación del movimiento de un coche en un espacio unidimensional:

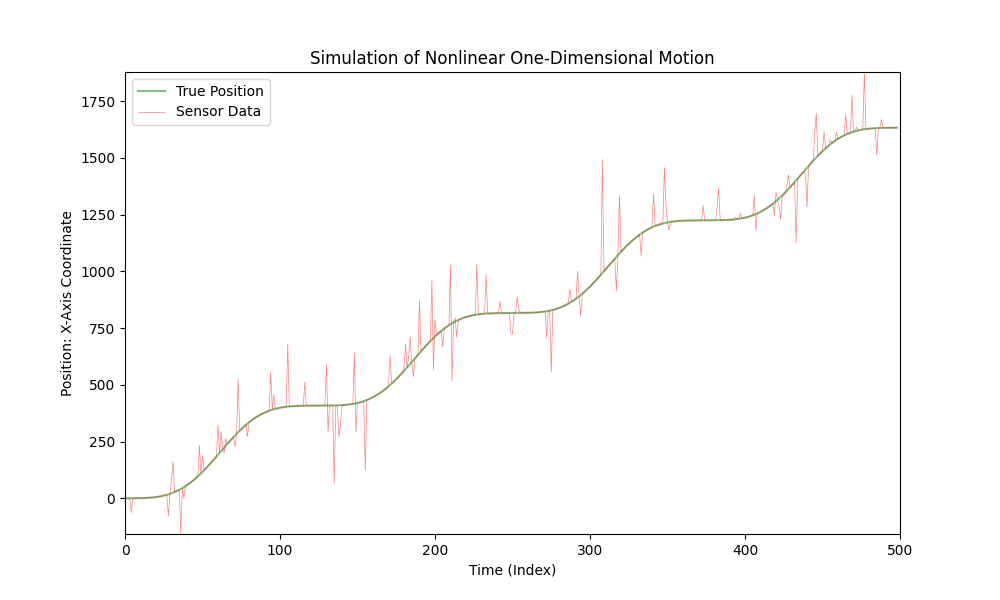
El coche se mueve con una aceleración variable y un sensor mide la coordenada X del coche. En esta simulación, añadimos ruido a los datos del sensor para tener en cuenta posibles errores de medición.

El código proporcionado anteriormente visualiza esta simulación, donde la línea verde representa la posición "verdadera" del automóvil, y la línea roja representa los datos del sensor, teniendo en cuenta el ruido añadido. La aceleración cambia con el tiempo, creando una simulación más realista del movimiento del automóvil.

Este código se puede utilizar para visualizar y analizar diferentes escenarios de movimiento de automóviles, considerando cambios en la aceleración y posibles errores de sensores.

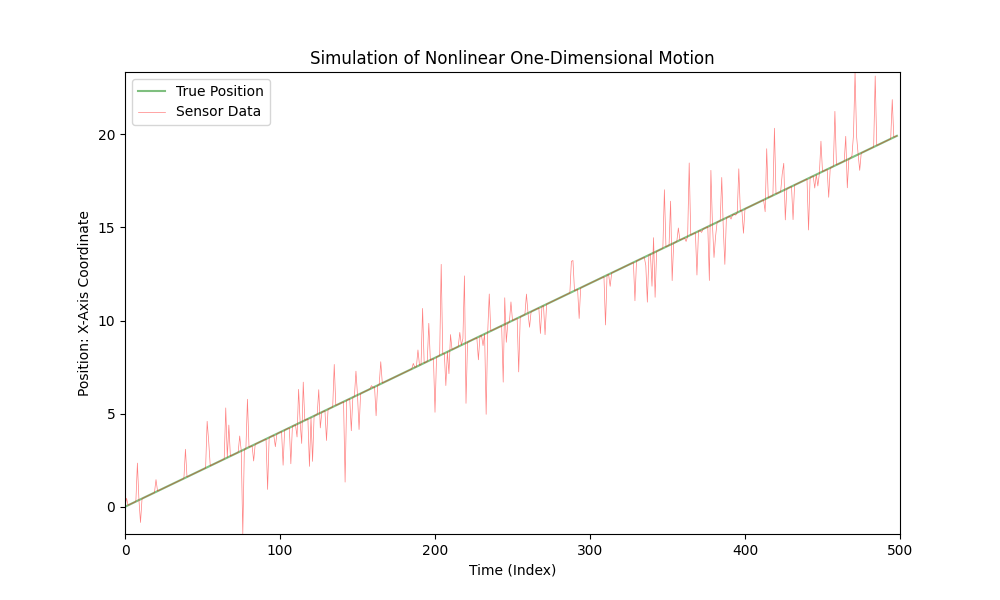
Para simular un movimiento lineal, simplemente puedes modificar la función nonlinear_acceleration(t) para que siempre devuelva 0:

def nonlinear_acceleration(t):
    return 0

Este cambio hará que el movimiento del coche sea lineal con velocidad constante.

El filtro de Kalman

El filtro de Kalman es un algoritmo desarrollado por Rudolf E. Kalman en 1960. Este algoritmo permite la estimación del estado de un sistema dinámico basado en un conjunto de mediciones incompletas y ruidosas. Inicialmente, el filtro de Kalman fue desarrollado para abordar problemas en la ingeniería aeroespacial, pero con el tiempo, ha encontrado aplicaciones amplias en diversos campos. La principal ventaja del filtro de Kalman es que es recursivo, lo que significa que utiliza las mediciones más recientes y el estado anterior para calcular el estado actual del sistema. Esto lo hace eficiente para el procesamiento de datos en tiempo real en línea.

El filtro de Kalman ha encontrado aplicaciones en muchos campos, incluyendo navegación y control de vehículos, procesamiento de señales, econometría, robótica y muchas otras áreas donde se requiere la estimación de procesos variables en el tiempo basada en datos imperfectos o incompletos.

El filtro de Kalman tiene varias ventajas clave sobre otros algoritmos de estimación y filtrado de datos:

Optimalidad: Bajo ciertas condiciones (sistema lineal, ruido gaussiano), el Filtro de Kalman es óptimo en términos de minimizar el error cuadrático medio de estimación.
Eficiencia en Tiempo Real: El Filtro de Kalman es recursivo, lo que significa que utiliza únicamente las mediciones más recientes y el estado anterior para calcular el estado actual. Esto lo hace adecuado para aplicaciones en tiempo real.
Requisito Mínimo de Memoria: Dado que el filtro solo utiliza la medición más reciente y la estimación del estado actual, no necesita almacenar el historial completo de datos.
Robustez ante Errores de Medición: El filtro es capaz de procesar eficientemente datos ruidosos, minimizando el impacto de errores de medición aleatorios.
Aplicaciones Versátiles: Debido a su versatilidad, el Filtro de Kalman ha sido aplicado en campos diversos, desde la ingeniería aeroespacial hasta la econometría.
Facilidad de Implementación: El algoritmo es relativamente fácil de entender e implementar, lo que lo hace accesible para una amplia gama de profesionales.

Implementemos un filtro de Kalman básico para un sensor que mide la posición de nuestro coche, el cual se mueve en un sistema unidimensional con velocidad constante pero con mediciones de sensor ruidosas.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
import sys
import random

# Read noise_percentage, noise_probability, total_points from the command line
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = 10 / total_points

# Initialize true positions and velocity
true_positions_linear = [0]
true_velocity = 2

for t in range(1, total_points):
    true_positions_linear.append(true_positions_linear[-1] + true_velocity * interval)

# Function to add noise to true positions
def add_noise(true_positions, probability):
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions))
            if random.uniform(0, 1) <= probability else p for p in true_positions]

sensor_positions_with_noise = add_noise(true_positions_linear, noise_probability)

# Initialize Kalman Filter (KF)
kf = KalmanFilter(dim_x=2, dim_z=1)
kf.F = np.array([[1, interval],
                 [0, 1]])
kf.H = np.array([[1, 0]])
kf.P *= 1000
kf.R = noise_percentage * np.mean(true_positions_linear)
kf.Q = Q_discrete_white_noise(dim=2, dt=interval, var=0.001)

x = np.array([[sensor_positions_with_noise[0]],
              [0]])
kf_positions = [x[0, 0]]

# Function to update Kalman Filter with sensor data
def update_kalman_filter(z):
    kf.predict()
    kf.update(z)
    return kf.x[0, 0]

# Function to create an animation with Kalman Filter (KF) estimation
def animate_with_kalman(i):
    plt.cla()
    plt.plot(true_positions_linear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, linewidth=0.5, label='Sensor Data')

    if i < total_points:
        kf_estimate = update_kalman_filter(sensor_positions_with_noise[i])
        kf_positions.append(kf_estimate)

    plt.plot(kf_positions[:i + 1], color='blue', alpha=0.5, label='Kalman Filter (KF) Estimate')

    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_linear + sensor_positions_with_noise),
             max(true_positions_linear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Linear One-Dimensional Motion with Kalman Filter (KF)')
    plt.legend()

# Main entry point
if __name__ == "__main__":
    # Create a figure and animation
    fig, ax = plt.subplots(figsize=(10, 6))
    ani = FuncAnimation(fig, animate_with_kalman, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

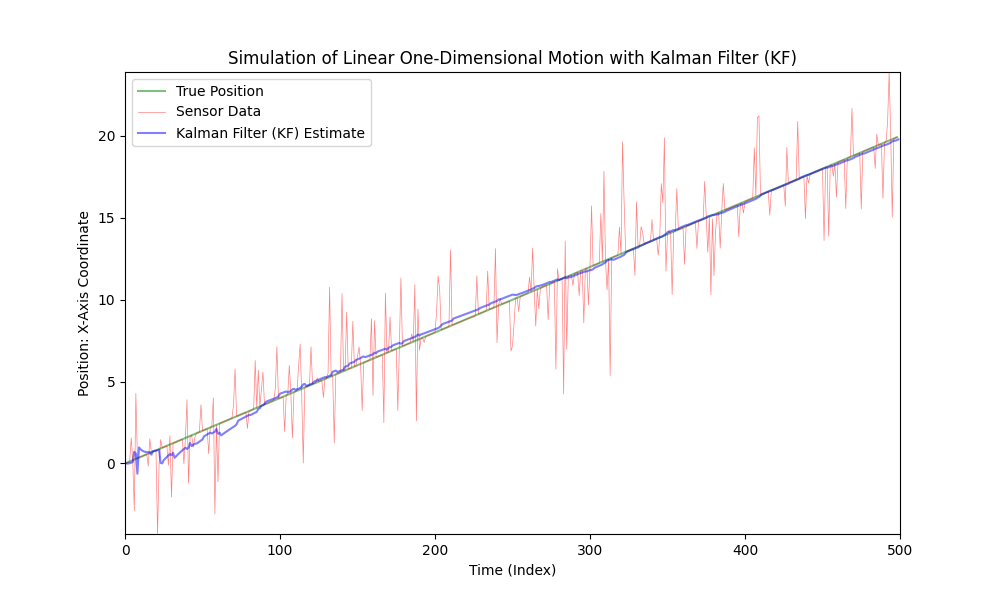
Como se ha visto, el Filtro de Kalman es adecuado para su uso en sistemas lineales incluso con ruido fuerte. Sin embargo, el movimiento del coche no es lineal; el coche acelera con magnitudes y direcciones variables.

Complicaremos un poco nuestro código haciendo que el movimiento del coche sea no lineal e introduciendo una aceleración variable. Por simplicidad y claridad, usaremos una función sinusoidal para modelar la aceleración. Mantendremos el nivel de ruido igual.

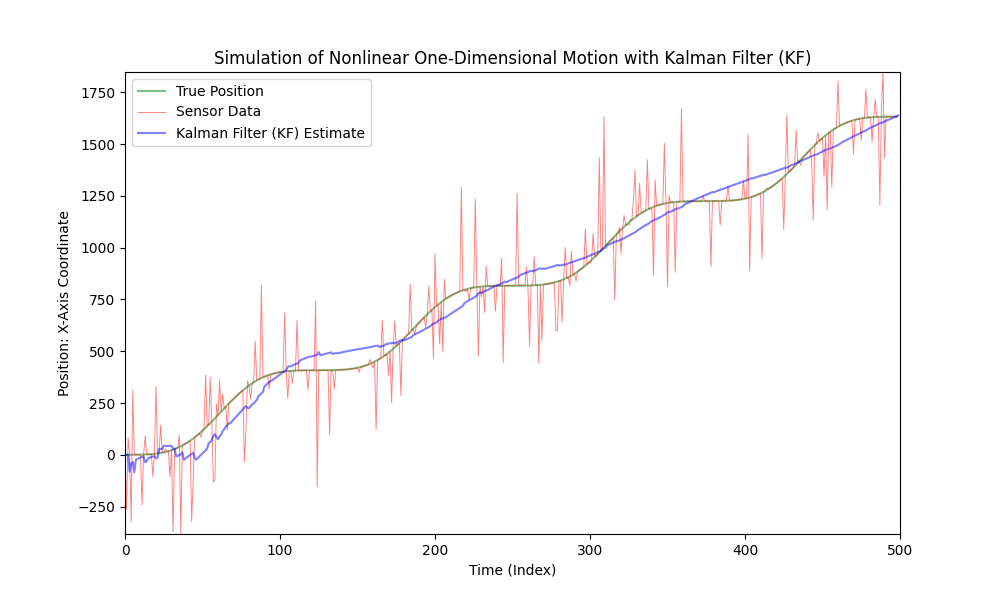
Como podemos ver, el filtro Kalman clásico no es adecuado para modelos no lineales. Para estos propósitos, se desarrolló el Filtro Kalman Extendido (EKF).

Filtro de Kalman Extendido (EKF)

El Filtro de Kalman Extendido (EKF) es una modificación del Filtro de Kalman clásico diseñado para trabajar con sistemas no lineales. Mientras que el Filtro de Kalman estándar está destinado para sistemas lineales, el EKF extiende su aplicabilidad para manejar casos no lineales.

El Filtro de Kalman Extendido se desarrolló después del Filtro de Kalman original, introducido por Rudolf Kalman en 1960. Surgió como resultado del esfuerzo de ingenieros y científicos por adaptar el Filtro de Kalman para su uso con sistemas no lineales, especialmente en los campos de navegación aeroespacial y marítima en las décadas de 1960 y 1970. La fecha precisa de su creación y los autores específicos son menos conocidos, ya que el EKF evolucionó gradualmente y dentro del marco de varios grupos de investigación.

El Filtro de Kalman Extendido (EKF) es ampliamente utilizado en tareas donde se requiere la estimación de estado de sistemas descritos por ecuaciones no lineales. Sus principales áreas de aplicación incluyen la robótica (para estimar la posición y orientación de robots), la industria automotriz (en sistemas de conducción autónoma y navegación), ingeniería aeroespacial (para la navegación orbital de satélites y naves espaciales), comunicaciones móviles y muchos otros campos técnicos e ingenieriles.

Las principales diferencias entre el Filtro de Kalman Extendido (EKF) y el Filtro de Kalman estándar radican principalmente en cómo manejan las dinámicas y mediciones del sistema.

Las principales distinciones incluyen lo siguiente:

Manejo de la No Linealidad: El Filtro de Kalman estándar asume que la dinámica del sistema y el proceso de medición son lineales. Esto significa que las funciones de transición de estado y de medición pueden representarse como matrices lineales. El Filtro de Kalman Extendido (EKF por sus siglas en inglés) está diseñado para trabajar con sistemas no lineales. En lugar de matrices lineales, utiliza funciones no lineales para describir la dinámica del sistema y el proceso de medición.
Linealización: En el EKF, la linealización se utiliza para aproximar funciones no lineales, típicamente mediante la expansión en series de Taylor de primer orden alrededor de la estimación actual del estado. Esto proporciona contrapartes linealizadas de las funciones de transición de estado y de medición, que luego se utilizan en el filtro.
Funciones de Transición de Estado y Medición: En el Filtro de Kalman estándar, las funciones de transición de estado y de medición están representadas por matrices (por ejemplo, matriz de transición de estado y matriz de medición). En el EKF, estas funciones pueden ser cualquier función no lineal diferenciable. Esto añade flexibilidad pero también aumenta la complejidad y los requisitos computacionales.
Complejidad Computacional: El EKF requiere una mayor complejidad computacional debido a la necesidad de linealizar funciones no lineales y los cálculos subsiguientes.

La principal diferencia entre el Filtro de Kalman Extendido y el estándar es su capacidad para trabajar con sistemas no lineales mediante el uso de funciones no lineales y su linearización.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
import sys
import random

# Named constants
AMPLITUDE_FACTOR = 5.0  # Factor for amplitude in the nonlinear acceleration function
WAVES = 4  # Number of waves in the nonlinear motion model
INITIAL_POSITION = 0  # Initial position
TRUE_VELOCITY_INITIAL = 2.0  # Initial true velocity (changed to float)
TRUE_VELOCITY_INCREMENT = 0.2  # Increment for true velocity (added as a constant)
PREDICTION_INTERVAL = 10  # Interval for predictions
DIM_X = 2  # Dimension of state vector in Kalman filter
DIM_Z = 1  # Dimension of measurement vector in Kalman filter
INITIAL_P_COVARIANCE = 1000  # Initial state covariance for Kalman filter

# Initialize random number generator with the current time
random.seed()

# Read noise_percentage, noise_probability, and total_points from command line arguments
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = PREDICTION_INTERVAL / total_points  # Time interval between data points

# Define a nonlinear acceleration function that varies with time
def nonlinear_acceleration(t):
    # Calculate the amplitude of acceleration based on time
    amplitude = AMPLITUDE_FACTOR * 200.0 * (1 - abs((t % (total_points / WAVES) - (total_points / (2 * WAVES))) / (total_points / (2 * WAVES))))
    # Calculate the nonlinear acceleration based on time and amplitude
    return amplitude * np.sin(2.0 * np.pi * t / (total_points / WAVES))

# Function to add noise to true positions with a given probability
def add_noise(true_positions, probability):
    # Add Gaussian noise to true positions with specified probability
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions)) if random.uniform(0, 1) <= probability else p for p in true_positions]

# Function to update the Extended Kalman Filter (EKF) with sensor measurements
def update_extended_kalman_filter(z):
    ekf.predict()  # Predict the next state
    ekf.update(z)  # Update the state based on sensor measurements
    return ekf.x[0, 0]  # Return the estimated position

# Функция для закрытия анимации при нажатии клавиши ESC
def close_animation(event):
    if event.key == 'escape':
        plt.close()

# Function for creating an animation with EKF estimates
def animate_with_ekf(i):
    plt.cla()
    # Plot the true position and sensor data up to the current time
    plt.plot(true_positions_nonlinear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, label='Sensor Data', linewidth=0.5)

    if i < total_points:
        # Update the EKF with the current sensor measurement and obtain the estimate
        ekf_estimate = update_extended_kalman_filter(sensor_positions_with_noise[i])
        ekf_positions.append(ekf_estimate)

    # Plot the EKF estimate up to the current time
    plt.plot(ekf_positions[:i + 1], color='purple', alpha=0.5, label='Extended Kalman Filter (EKF) Estimate')

    # Set plot limits and labels
    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_nonlinear + sensor_positions_with_noise),
             max(true_positions_nonlinear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Nonlinear One-Dimensional Motion with Extended Kalman Filter (EKF)')
    plt.legend()

# Main entry point of the code
if __name__ == "__main__":
    # Create a figure for the animation
    fig, ax = plt.subplots(figsize=(10, 6))

    # Используйте connect для добавления обработчика событий
    fig.canvas.mpl_connect('key_press_event', close_animation)

    # Initialize true_positions_nonlinear with the initial position and true_velocity
    true_positions_nonlinear = [INITIAL_POSITION]
    true_velocity = TRUE_VELOCITY_INITIAL

    # Generate true positions based on the nonlinear motion model
    for t in range(1, total_points):
        acc = nonlinear_acceleration(t)
        true_velocity += acc * interval
        true_positions_nonlinear.append(true_positions_nonlinear[-1] + true_velocity * interval)

    # Add noise to true positions to simulate sensor data
    sensor_positions_with_noise = add_noise(true_positions_nonlinear, noise_probability)

    # Initialize an Extended Kalman Filter (EKF)
    ekf = KalmanFilter(dim_x=DIM_X, dim_z=DIM_Z)
    ekf.F = np.array([[1, interval],
                    [0, 1]])
    ekf.H = np.array([[1, 0]])
    ekf.P *= INITIAL_P_COVARIANCE
    ekf.R = noise_percentage * np.mean(true_positions_nonlinear)

    ekf_x = np.array([[sensor_positions_with_noise[0]],
                    [0]])
    ekf_positions = [ekf_x[0, 0]]

    # Create the animation using FuncAnimation
    ani = FuncAnimation(fig, animate_with_ekf, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

Aplica el filtro de Kalman extendido para el movimiento no lineal.

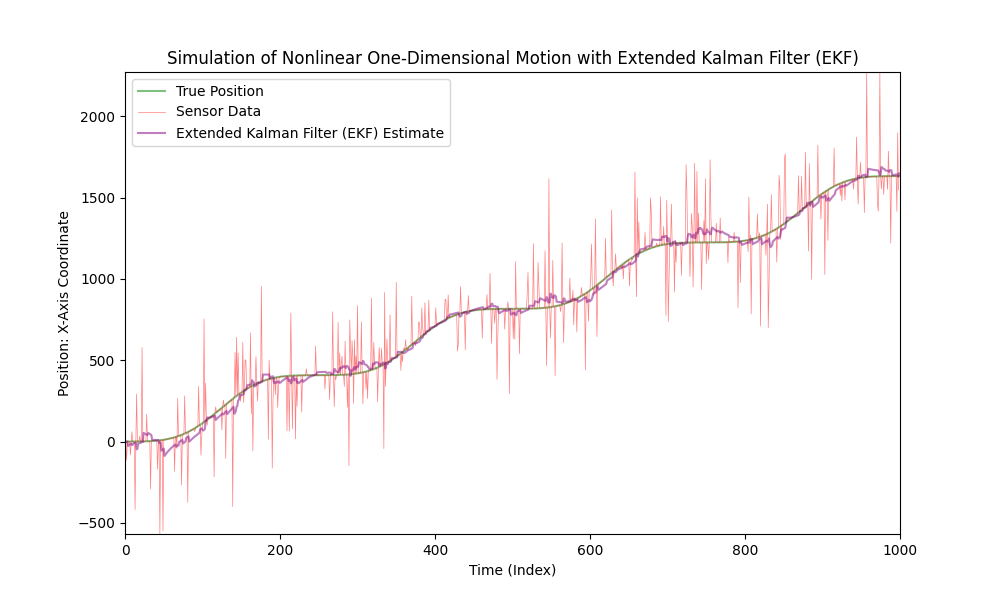
Ahora, aumentemos significativamente el nivel de ruido del sensor.

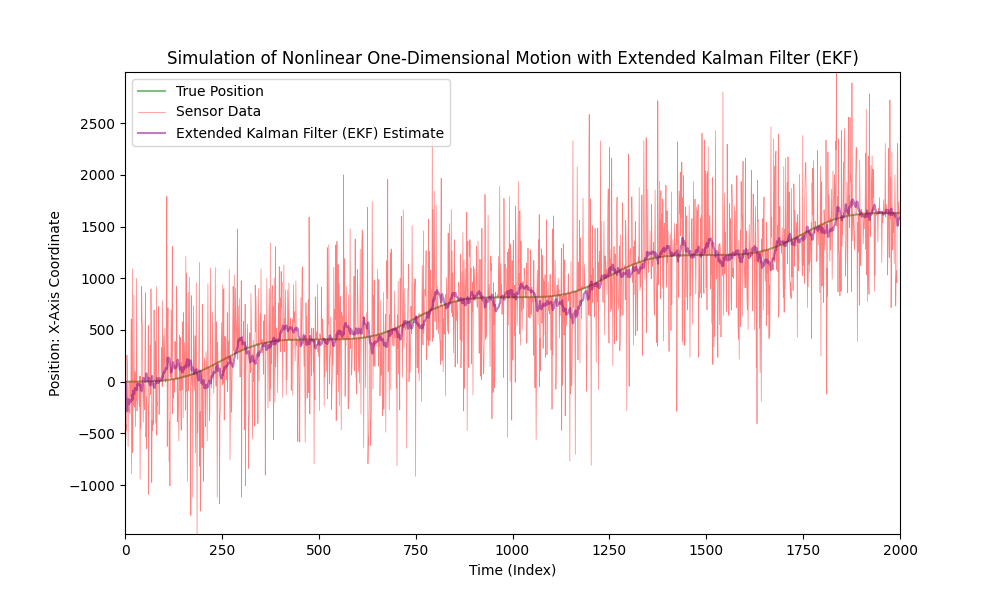
Como podemos ver, el Filtro de Kalman Extendido funciona bien incluso en casos de datos altamente ruidosos.

Materiales adicionales

https://en.wikipedia.org/wiki/Kalman_filter - Descripción del filtro y sus principios matemáticos fundamentales de funcionamiento.

https://kalmanfilter.org/cpp/index.html - Descripción e implementación del filtro en C++.

https://commons.apache.org/proper/commons-math/javadocs/api-3.6.1/org/apache/commons/math3/filter/KalmanFilter.html - Descripción e implementación del filtro en Java.

https://filterpy.readthedocs.io/en/latest/kalman/KalmanFilter.html - Descripción e implementación del filtro en Python

Conclusión

El Filtro de Kalman Extendido (EKF) es una herramienta poderosa para estimar el estado de sistemas dinámicos, especialmente cuando esta estimación necesita basarse en datos de múltiples sensores simultáneamente. Una de las principales ventajas del EKF es su capacidad para integrar información de diversas fuentes, lo que lo hace excepcionalmente útil en sistemas complejos como sistemas de navegación automotriz, robótica o ingeniería aeroespacial.

Considerando datos ruidosos y a menudo imperfectos de diferentes sensores, el EKF es capaz de fusionar estos datos en un conjunto unificado, proporcionando una estimación de estado más precisa y confiable. Por ejemplo, en un automóvil, el EKF puede usar datos de GPS para determinar la posición y datos del acelerómetro para calcular la velocidad y la aceleración, creando así una imagen más completa del movimiento del vehículo.

El Filtro de Kalman Extendido (EKF) es capaz de reducir la incertidumbre general que surge del ruido y los errores de cada sensor individual. Dado que estos errores a menudo no están correlacionados, su procesamiento conjunto en el EKF permite obtener estimaciones más estables y precisas. También es importante señalar que el EKF exhibe una alta robustez: en caso de problemas con uno de los sensores, el sistema puede continuar operando confiando en los datos de los demás. Esto hace que el EKF sea particularmente valioso en aplicaciones críticas donde la fiabilidad y la precisión son de suma importancia. Otro aspecto importante al trabajar con múltiples sensores es la sincronización temporal de las mediciones. El EKF maneja hábilmente estas diferencias temporales, asegurando una correcta fusión de datos.

Gracias a su capacidad de agrupar y analizar información de múltiples fuentes, el EKF es una herramienta invaluable en áreas donde se requiere una estimación de estado de alta precisión bajo condiciones de incertidumbre y cambios dinámicos.

En conclusión, el software que combate el ruido de los sensores es un proceso desafiante que abarca métodos estáticos y estadísticos y la aplicación de inteligencia artificial para la clasificación y mitigación de tipos de ruido.

Nuestra empresa posee una amplia experiencia en el manejo de problemas de ruido en sensores.

Para consultas relacionadas con este artículo, no dudes en contactarnos en articles@stofu.io.

Para oportunidades de colaboración, puedes contactarnos en info@stofu.io.

Todos los archivos de código los puedes encontrar en nuestro repositorio: https://github.com/SToFU-Systems/EKF_Usage.

Deseándote todo lo mejor,

Equipo de Sistemas SToFU

https://stofu.io

Enfoque de software para tratar el ruido de los sensores ADAS (Parte 1)

¿Qué es ADAS?

Ruido del Sensor en ADAS

Simulación del Movimiento de un Punto en un Sistema de Coordenadas Unidimensional

El filtro de Kalman

Filtro de Kalman Extendido (EKF)

Materiales adicionales

Conclusión

Categorías

Noticias recientes

Enfoque de software para tratar el ruido de los sensores ADAS (Parte 1)

Analizador de Recursos PE en C++ (Nativo)

Introducción al Desarrollo del Kernel de Windows en Rust (Parte 1)

Introducción a la programación de GPU

Dentro de BlackMatter: Análisis Técnico del Ransomware BlackMatter