Programvaruansats för att hantera ljud från ADAS-sensorer (Del 1)

Vad är ADAS?

Moderna bilar blir allt smartare tack vare ADAS (Advanced Driver Assistance Systems) som förbättrar vägsäkerheten och gör körningen mer komfortabel. Dessa system, som använder kameror, radar och andra sensorer, hjälper till med fordonskontroll, upptäcker andra fordon, fotgängare och trafikljussignaler, och ger föraren aktuell information om vägförhållandena och den omgivande miljön.

ADAS inkluderar olika funktioner som adaptiv farthållare, som justerar bilens hastighet till trafiken framför, filhanteringssystem för att hålla bilen i sin fil, automatisk bromsning för att förebygga kollisioner och automatiska parkeringssystem för att underlätta parkeringsmanövrar. Olika typer av sensorer, såsom kameror, radar, lidar och ultraljudssensorer, säkerställer funktionen hos dessa system, vilket hjälper bilen att anpassa sig till vägförhållandena och förarens körstil.

Sensorbrus i ADAS

ADAS-sensorer, trots deras modernitet och komplexitet, är känsliga för störningar. Detta beror på flera orsaker. För det första kan miljön ha oförutsägbara effekter på sensorerna. Till exempel kan smuts, damm, regn eller snö täcka kameror och radar, vilket förvränger den information de tar emot. Det är som att försöka titta genom smutsigt glas: inte allt är synligt och inte lika klart, och vyn blockeras av många artefakter. För det andra kan även sensorernas tekniska begränsningar leda till brus. Till exempel kan sensorer fungera dåligt i svagt ljus eller i starka ljuskontraster. Det är som att försöka urskilja något i mörkret eller titta på en överdrivet ljus ljuskälla – i båda fallen blir det extremt svårt att se detaljer. När den data som tas emot från sensorerna är förvrängd, kan förarassistanssystemet feltolka vägsituationen, vilket i vissa situationer kan öka risken för trafikolyckor.

Simulering av punktrörelse i ett endimensionellt koordinatsystem

För att börja, låt oss skriva koden för att simulera rörelsen av en bil i ett endimensionellt rum. För att köra koden behöver du sätta upp en Python-miljö och installera nödvändiga bibliotek.

Här är stegen för att installera biblioteken och köra koden:

För att köra koden måste du ställa in en Python-miljö och installera nödvändiga bibliotek. Här är stegen för att installera biblioteken och köra koden: Installera Python: Om du inte har Python än, ladda ner och installera det från den officiella Python-webbplatsen (https://www.python.org/downloads/). Det rekommenderas att använda Python version 3.x.
Installera nödvändiga bibliotek: Öppna kommandotolken (i Windows kan det vara kommandotolken eller PowerShell) och utför följande kommando för att installera biblioteken:
```
pip install matplotlib numpy filterpy
```
Spara din kod: Kopiera koden du angav och spara den i en fil med tillägget .py (till exempel simulation.py)
Kör koden: I kommandotolken, navigera till katalogen där din kodfil är placerad och exekvera den med följande kommando:
```
python simulation.py 20 20 500
```
Detta kommando kommer att köra koden med argumenten 20 (för brusamplitud), 20 (för brusfrekvens), och 500 (för det totala antalet datapunkter på grafen). Du kan ändra argumentvärdena efter behov.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
import sys
import random
import time

# Named constants
AMPLITUDE_FACTOR = 5.0  # Factor for amplitude in the nonlinear acceleration function
WAVES = 4  # Number of waves in the nonlinear motion model
INITIAL_POSITION = 0  # Initial position
TRUE_VELOCITY_INITIAL = 2.0  # Initial true velocity (changed to float)
TRUE_VELOCITY_INCREMENT = 0.2  # Increment for true velocity (added as a constant)
PREDICTION_INTERVAL = 10  # Interval for predictions
DIM_X = 2  # Dimension of state vector in Kalman filter
DIM_Z = 1  # Dimension of measurement vector in Kalman filter
INITIAL_P_COVARIANCE = 1000  # Initial state covariance for Kalman filter
RANDOM_SEED = 42  # Seed for random number generator

# Initialize random number generator with the current time
random.seed(int(time.time()))  # Using the current time to initialize the random number generator

# Read noise_percentage, noise_probability, and total_points from command line arguments
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = PREDICTION_INTERVAL / total_points  # Time interval between data points

# Define a nonlinear acceleration function that varies with time
def nonlinear_acceleration(t):
    # Calculate the amplitude of acceleration based on time
    amplitude = AMPLITUDE_FACTOR * 200.0 * (1 - abs((t % (total_points / WAVES) - (total_points / (2 * WAVES))) / (total_points / (2 * WAVES))))
    # Calculate the nonlinear acceleration based on time and amplitude
    return amplitude * np.sin(2.0 * np.pi * t / (total_points / WAVES))

# Function to add noise to true positions with a given probability
def add_noise(true_positions, probability):
    # Add Gaussian noise to true positions with specified probability
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions)) if random.uniform(0, 1) <= probability else p for p in true_positions]

# Function to close the animation on pressing the ESC key
def close_animation(event):
    if event.key == 'escape':
        plt.close()

# Function for creating an animation without the Kalman Filter
def animate_without_ekf(i):
    plt.cla()
    # Plot the true position and sensor data up to the current time
    plt.plot(true_positions_nonlinear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, label='Sensor Data', linewidth=0.5)

    # Set plot limits and labels
    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_nonlinear + sensor_positions_with_noise),
             max(true_positions_nonlinear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Nonlinear One-Dimensional Motion')

    # Display the legend
    plt.legend()

# Main entry point of the code
if __name__ == "__main__":
    # Create a figure for the animation
    fig, ax = plt.subplots(figsize=(10, 6))

    # Use connect to add an event handler for key presses
    fig.canvas.mpl_connect('key_press_event', close_animation)

    # Initialize true_positions_nonlinear with the initial position and true_velocity
    true_positions_nonlinear = [INITIAL_POSITION]
    true_velocity = TRUE_VELOCITY_INITIAL

    # Generate true positions based on the nonlinear motion model
    for t in range(1, total_points):
        acc = nonlinear_acceleration(t)
        true_velocity += acc * interval
        true_positions_nonlinear.append(true_positions_nonlinear[-1] + true_velocity * interval)

    # Add noise to true positions to simulate sensor data
    sensor_positions_with_noise = add_noise(true_positions_nonlinear, noise_probability)

    # Create the animation using FuncAnimation
    ani = FuncAnimation(fig, animate_without_ekf, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

Detta är en simulering av en bils rörelse i ett endimensionellt rum:

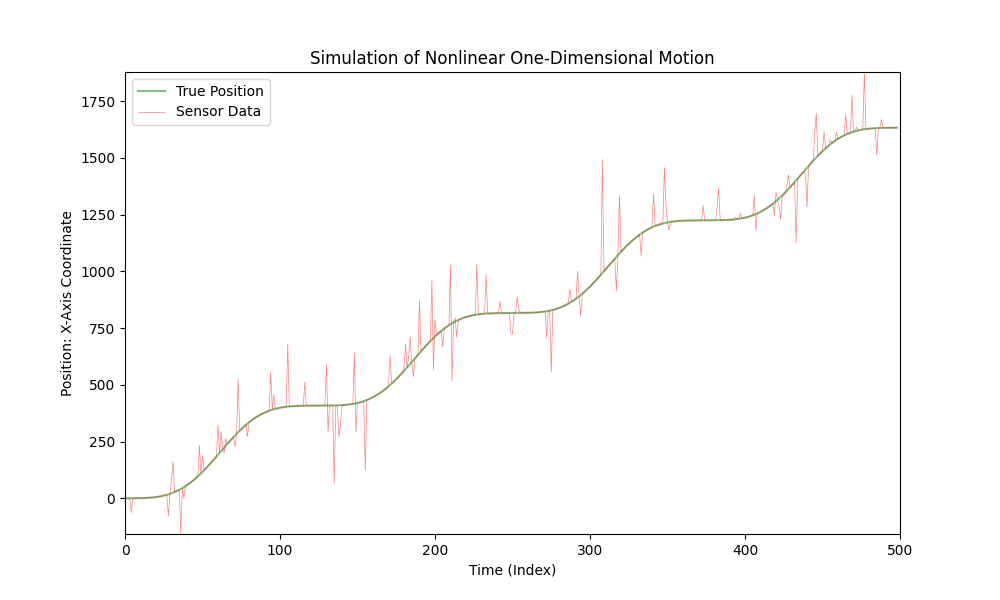
Bilen rör sig med varierande acceleration, och en sensor mäter bilens X-koordinat. I denna simulering lägger vi till brus i sensordatan för att ta hänsyn till möjliga mätfel.

Koden som tillhandahölls tidigare visualiserar denna simulering, där den gröna linjen representerar bilens "sanna" position, och den röda linjen representerar sensordata, med hänsyn till det tillagda bruset. Accelerationen ändras över tid, vilket skapar en mer realistisk simulering av bilens rörelse.

Denna kod kan användas för att visualisera och analysera olika scenarier av bilrörelse, med beaktande av föränderlig acceleration och möjliga sensorfel.

För att simulera linjär rörelse kan du enkelt modifiera funktionen nonlinear_acceleration(t) så att den alltid returnerar 0:

def nonlinear_acceleration(t):
    return 0

Denna ändring kommer att göra bilens rörelse linjär med konstant hastighet.

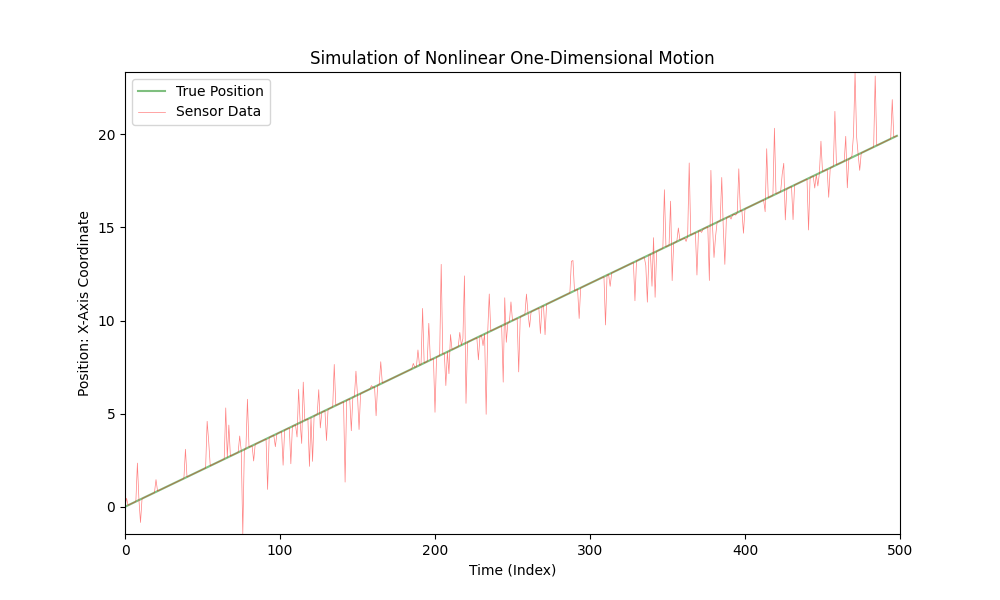
Kalmanfiltret

Kalmanfiltret är en algoritm som utvecklades av Rudolf E. Kalman år 1960. Denna algoritm möjliggör uppskattning av tillståndet för ett dynamiskt system baserat på en uppsättning ofullständiga och brusiga mätningar. Ursprungligen utvecklades Kalmanfiltret för att hantera problem inom rymdteknik, men med tiden har det funnit breda tillämpningar inom olika områden. Den främsta fördelen med Kalmanfiltret är att det är rekursivt, vilket innebär att det använder de senaste mätningarna och det tidigare tillståndet för att beräkna systemets nuvarande tillstånd. Detta gör det effektivt för onlinebehandling av realtidsdata.

Kalman-filtret har hittat tillämpningar inom många områden, inklusive navigation och fordonskontroll, signalbehandling, ekonometri, robotik och många andra områden där uppskattning av tidsvariabla processer baserade på ofullständig eller ofullständig data krävs.

Kalmanfiltret har flera nyckelfördelar jämfört med andra algoritmer för uppskattning och filtrering av data:

Optimalitet: Under vissa förhållanden (linjärt system, Gaussiskt brus), är Kalman-filter optimalt när det gäller att minimera medelkvadratiskt estimeringsfel.
Realtidseffektivitet: Kalman-filtret är rekursivt, vilket innebär att det endast använder de senaste mätningarna och det föregående tillståndet för att beräkna det aktuella tillståndet. Detta gör det lämpligt för realtidsapplikationer.
Minimalt minneskrav: Eftersom filtret endast använder den senaste mätningen och den aktuella tillståndsbedömningen behöver det inte lagra hela datahistoriken.
Robusthet mot mätfel: Filtret kan effektivt bearbeta brusiga data, vilket minimerar effekten av slumpmässiga mätfel.
Mångsidiga tillämpningar: På grund av sin mångsidighet har Kalman-filtret tillämpats inom diverse områden, från rymdteknik till ekonometri.
Lätt att implementera: Algoritmen är relativt enkel att förstå och implementera, vilket gör den tillgänglig för ett brett utbud av yrkesverksamma.

Låt oss implementera ett grundläggande Kalman-filter för en sensor som mäter positionen på vår bil, som rör sig i ett endimensionellt system med konstant hastighet men med bullriga sensormätningar.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
import sys
import random

# Read noise_percentage, noise_probability, total_points from the command line
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = 10 / total_points

# Initialize true positions and velocity
true_positions_linear = [0]
true_velocity = 2

for t in range(1, total_points):
    true_positions_linear.append(true_positions_linear[-1] + true_velocity * interval)

# Function to add noise to true positions
def add_noise(true_positions, probability):
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions))
            if random.uniform(0, 1) <= probability else p for p in true_positions]

sensor_positions_with_noise = add_noise(true_positions_linear, noise_probability)

# Initialize Kalman Filter (KF)
kf = KalmanFilter(dim_x=2, dim_z=1)
kf.F = np.array([[1, interval],
                 [0, 1]])
kf.H = np.array([[1, 0]])
kf.P *= 1000
kf.R = noise_percentage * np.mean(true_positions_linear)
kf.Q = Q_discrete_white_noise(dim=2, dt=interval, var=0.001)

x = np.array([[sensor_positions_with_noise[0]],
              [0]])
kf_positions = [x[0, 0]]

# Function to update Kalman Filter with sensor data
def update_kalman_filter(z):
    kf.predict()
    kf.update(z)
    return kf.x[0, 0]

# Function to create an animation with Kalman Filter (KF) estimation
def animate_with_kalman(i):
    plt.cla()
    plt.plot(true_positions_linear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, linewidth=0.5, label='Sensor Data')

    if i < total_points:
        kf_estimate = update_kalman_filter(sensor_positions_with_noise[i])
        kf_positions.append(kf_estimate)

    plt.plot(kf_positions[:i + 1], color='blue', alpha=0.5, label='Kalman Filter (KF) Estimate')

    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_linear + sensor_positions_with_noise),
             max(true_positions_linear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Linear One-Dimensional Motion with Kalman Filter (KF)')
    plt.legend()

# Main entry point
if __name__ == "__main__":
    # Create a figure and animation
    fig, ax = plt.subplots(figsize=(10, 6))
    ani = FuncAnimation(fig, animate_with_kalman, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

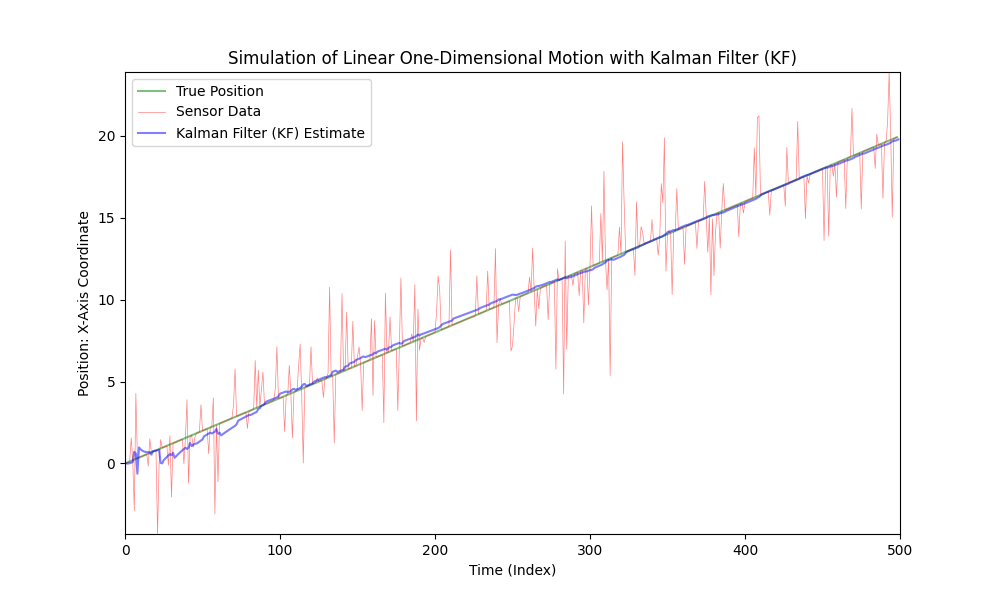
Som sett är Kalmanfiltret väl lämpat för användning i linjära system även med starkt brus. Däremot är bilens rörelse inte linjär; bilen accelererar med varierande storlekar och riktningar.

Låt oss komplicera vår kod lite genom att göra bilens rörelse icke-linjär och introducera variabel acceleration. För enkelhetens och tydlighetens skull kommer vi att använda en sinusfunktion för att modellera accelerationen. Vi kommer att behålla samma nivå av brus.

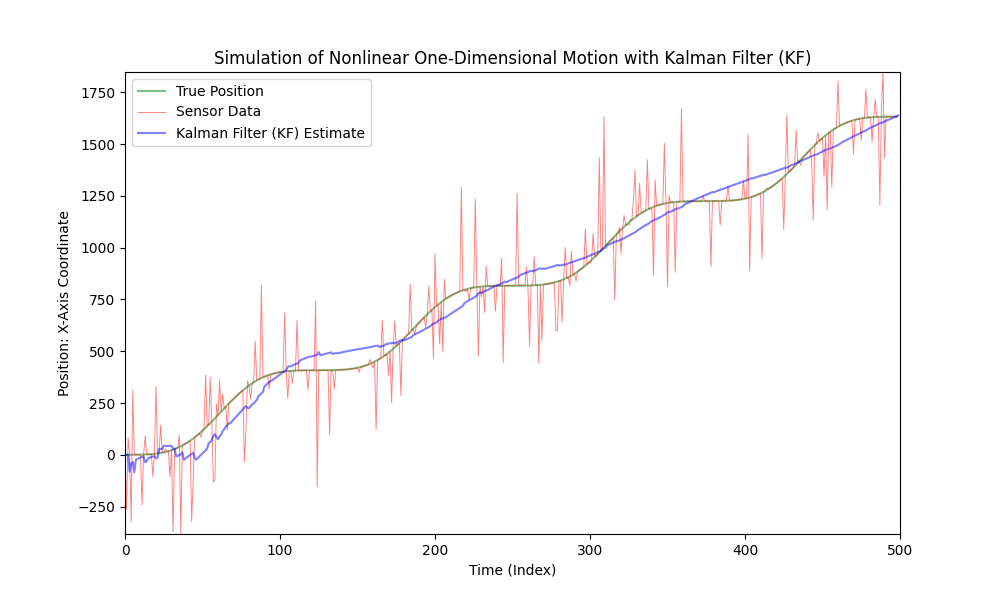
Som vi kan se är den klassiska Kalman-filtret inte lämpligt för icke-linjära modeller. För dessa ändamål utvecklades det utökade Kalman-filtret (EKF).

Extended Kalman Filter (EKF)

The Extended Kalman Filter (EKF) är en modifiering av det klassiska Kalman-filtret som är utformat för att fungera med icke-linjära system. Medan det standard Kalman-filtret är avsett för linjära system, utvidgar EKF dess användbarhet för att hantera icke-linjära fall.

Extended Kalman Filter utvecklades efter det ursprungliga Kalman Filter, som introducerades av Rudolf Kalman 1960. Det uppstod som ett resultat av ansträngningar av ingenjörer och forskare för att anpassa Kalman Filter för användning med icke-linjära system, särskilt inom rymd- och sjöfartsnavigering under 1960- och 1970-talen. Det exakta datumet för dess skapande och specifika författare är mindre välkända, eftersom EKF utvecklades gradvis och inom ramen för olika forskargrupper.

Den Extended Kalman Filter (EKF) används flitigt i uppgifter där tillståndsuppskattning av system beskrivna av icke-linjära ekvationer krävs. Dess huvudsakliga tillämpningsområden inkluderar robotik (för uppskattning av position och orientering hos robotar), fordonsindustrin (i autonoma körsystem och navigation), rymdteknik (för navigering av satellitbanor och rymdfarkoster), mobilkommunikation, samt många andra tekniska och ingenjörsmässiga fält.

De huvudsakliga skillnaderna mellan Extended Kalman Filter (EKF) och det standard Kalman Filter ligger främst i hur de hanterar systemets dynamik och mätningar.

De främsta skillnaderna inkluderar följande:

Hantering av icke-linjäritet: Den standardiserade Kalmanfiltret antar att systemdynamiken och mätningsprocessen är linjära. Detta innebär att tillståndsövergång och mätningsfunktioner kan representeras som linjära matriser. Det Utökade Kalmanfiltret (EKF) är utformat för att fungera med icke-linjära system. Istället för linjära matriser används icke-linjära funktioner för att beskriva systemdynamiken och mätningsprocessen.
Linearisering: I EKF används linearisering för att approximera icke-linjära funktioner, vanligtvis genom expansion av Taylorserien av första ordningen runt den aktuella uppskattningen av tillståndet. Detta ger lineariserade motsvarigheter till tillståndsövergångs- och mätningsfunktionerna, som sedan används i filtret.
Tillståndsövergångs och mätningsfunktioner: I det standardiserade Kalmanfiltret representeras tillståndsövergångs- och mätningsfunktionerna av matriser (t.ex. tillståndsövergångsmatris och mätningsmatris). I EKF kan dessa funktioner vara vilka differentierbara icke-linjära funktioner som helst. Detta tillför flexibilitet men ökar också komplexiteten och beräkningskraven.
Beräkningskomplexitet: EKF kräver högre beräkningskomplexitet på grund av behovet av att linearisera icke-linjära funktioner och efterföljande beräkningar.

Den huvudsakliga skillnaden mellan Extended Kalman Filter och det standard är dess förmåga att arbeta med icke-linjära system genom att använda icke-linjära funktioner och deras linjärisering.

#
#  Copyright (C) 2024, SToFU Systems S.L.
#  All rights reserved.
#
#  This program is free software; you can redistribute it and/or modify
#  it under the terms of the GNU General Public License as published by
#  the Free Software Foundation; either version 3 of the License, or
#  (at your option) any later version.
#
#  This program is distributed in the hope that it will be useful,
#  but WITHOUT ANY WARRANTY; without even the implied warranty of
#  MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
#  GNU General Public License for more details.
#
#  You should have received a copy of the GNU General Public License along
#  with this program; if not, write to the Free Software Foundation, Inc.,
#  51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
#

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
from filterpy.kalman import KalmanFilter
from filterpy.common import Q_discrete_white_noise
import sys
import random

# Named constants
AMPLITUDE_FACTOR = 5.0  # Factor for amplitude in the nonlinear acceleration function
WAVES = 4  # Number of waves in the nonlinear motion model
INITIAL_POSITION = 0  # Initial position
TRUE_VELOCITY_INITIAL = 2.0  # Initial true velocity (changed to float)
TRUE_VELOCITY_INCREMENT = 0.2  # Increment for true velocity (added as a constant)
PREDICTION_INTERVAL = 10  # Interval for predictions
DIM_X = 2  # Dimension of state vector in Kalman filter
DIM_Z = 1  # Dimension of measurement vector in Kalman filter
INITIAL_P_COVARIANCE = 1000  # Initial state covariance for Kalman filter

# Initialize random number generator with the current time
random.seed()

# Read noise_percentage, noise_probability, and total_points from command line arguments
noise_percentage = float(sys.argv[1]) / 100.0 if len(sys.argv) > 1 else 0.1
noise_probability = float(sys.argv[2]) / 100.0 if len(sys.argv) > 2 else 0.2
total_points = int(sys.argv[3]) if len(sys.argv) > 3 else 2000
interval = PREDICTION_INTERVAL / total_points  # Time interval between data points

# Define a nonlinear acceleration function that varies with time
def nonlinear_acceleration(t):
    # Calculate the amplitude of acceleration based on time
    amplitude = AMPLITUDE_FACTOR * 200.0 * (1 - abs((t % (total_points / WAVES) - (total_points / (2 * WAVES))) / (total_points / (2 * WAVES))))
    # Calculate the nonlinear acceleration based on time and amplitude
    return amplitude * np.sin(2.0 * np.pi * t / (total_points / WAVES))

# Function to add noise to true positions with a given probability
def add_noise(true_positions, probability):
    # Add Gaussian noise to true positions with specified probability
    return [p + np.random.normal(0, scale=noise_percentage * np.mean(true_positions)) if random.uniform(0, 1) <= probability else p for p in true_positions]

# Function to update the Extended Kalman Filter (EKF) with sensor measurements
def update_extended_kalman_filter(z):
    ekf.predict()  # Predict the next state
    ekf.update(z)  # Update the state based on sensor measurements
    return ekf.x[0, 0]  # Return the estimated position

# Функция для закрытия анимации при нажатии клавиши ESC
def close_animation(event):
    if event.key == 'escape':
        plt.close()

# Function for creating an animation with EKF estimates
def animate_with_ekf(i):
    plt.cla()
    # Plot the true position and sensor data up to the current time
    plt.plot(true_positions_nonlinear[:i], color='green', alpha=0.5, label='True Position')
    plt.plot(sensor_positions_with_noise[:i], color='red', alpha=0.5, label='Sensor Data', linewidth=0.5)

    if i < total_points:
        # Update the EKF with the current sensor measurement and obtain the estimate
        ekf_estimate = update_extended_kalman_filter(sensor_positions_with_noise[i])
        ekf_positions.append(ekf_estimate)

    # Plot the EKF estimate up to the current time
    plt.plot(ekf_positions[:i + 1], color='purple', alpha=0.5, label='Extended Kalman Filter (EKF) Estimate')

    # Set plot limits and labels
    plt.xlim(0, total_points)
    plt.ylim(min(true_positions_nonlinear + sensor_positions_with_noise),
             max(true_positions_nonlinear + sensor_positions_with_noise))
    plt.xlabel('Time (Index)')
    plt.ylabel('Position: X-Axis Coordinate')
    plt.title('Simulation of Nonlinear One-Dimensional Motion with Extended Kalman Filter (EKF)')
    plt.legend()

# Main entry point of the code
if __name__ == "__main__":
    # Create a figure for the animation
    fig, ax = plt.subplots(figsize=(10, 6))

    # Используйте connect для добавления обработчика событий
    fig.canvas.mpl_connect('key_press_event', close_animation)

    # Initialize true_positions_nonlinear with the initial position and true_velocity
    true_positions_nonlinear = [INITIAL_POSITION]
    true_velocity = TRUE_VELOCITY_INITIAL

    # Generate true positions based on the nonlinear motion model
    for t in range(1, total_points):
        acc = nonlinear_acceleration(t)
        true_velocity += acc * interval
        true_positions_nonlinear.append(true_positions_nonlinear[-1] + true_velocity * interval)

    # Add noise to true positions to simulate sensor data
    sensor_positions_with_noise = add_noise(true_positions_nonlinear, noise_probability)

    # Initialize an Extended Kalman Filter (EKF)
    ekf = KalmanFilter(dim_x=DIM_X, dim_z=DIM_Z)
    ekf.F = np.array([[1, interval],
                    [0, 1]])
    ekf.H = np.array([[1, 0]])
    ekf.P *= INITIAL_P_COVARIANCE
    ekf.R = noise_percentage * np.mean(true_positions_nonlinear)

    ekf_x = np.array([[sensor_positions_with_noise[0]],
                    [0]])
    ekf_positions = [ekf_x[0, 0]]

    # Create the animation using FuncAnimation
    ani = FuncAnimation(fig, animate_with_ekf, frames=total_points, interval=interval * 1000, repeat=False)

    # Display the animation
    plt.show()

Använd Extended Kalman Filter för icke-linjär rörelse.

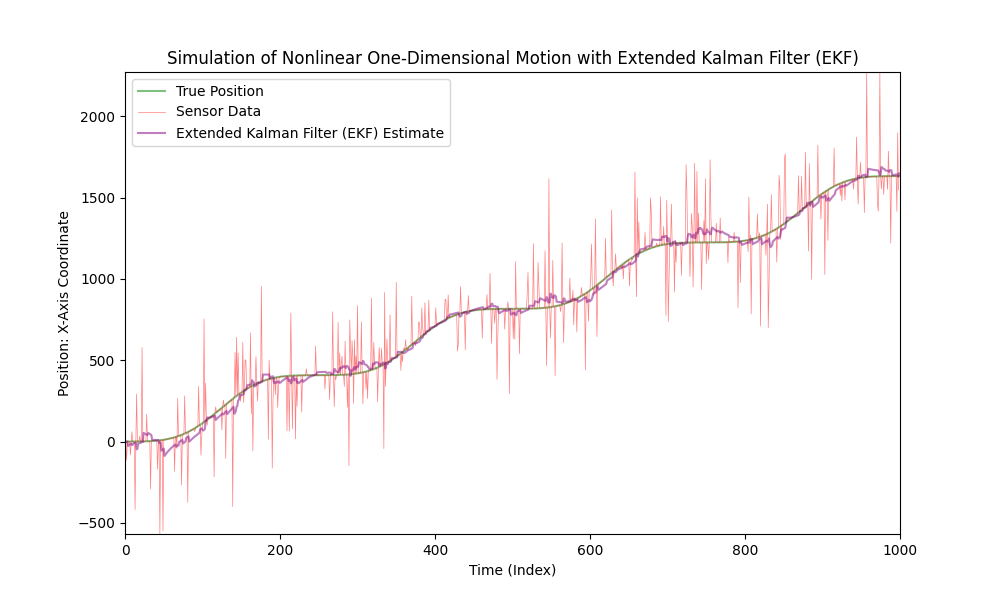
Nu ska vi avsevärt öka nivån av sensorsus.

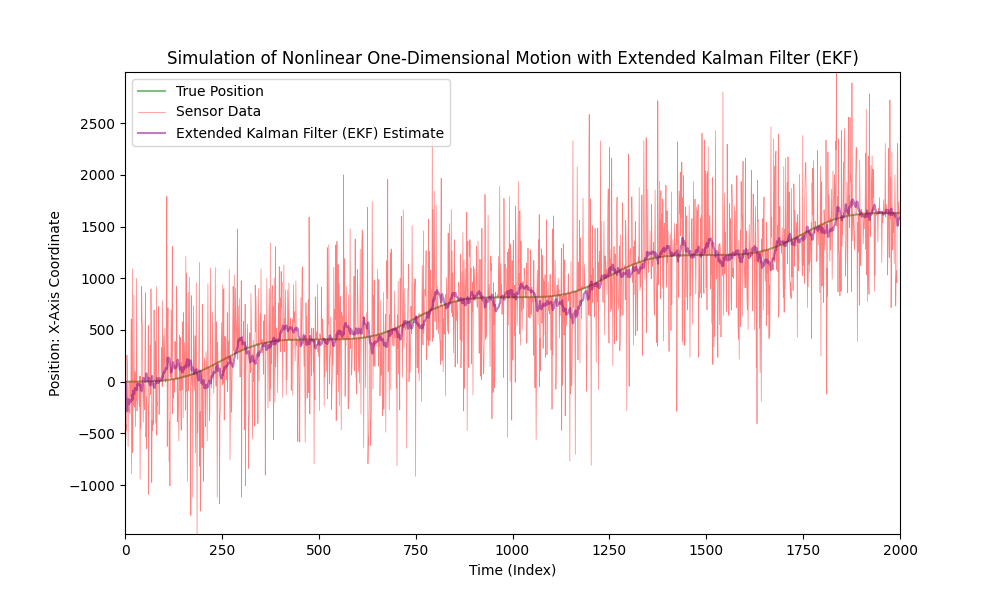
Som vi kan se, presterar Extended Kalman Filter bra även i fall av mycket brusiga data.

Ytterligare material

https://en.wikipedia.org/wiki/Kalman_filter - Beskrivning av filtret och dess grundläggande matematiska principer för funktion.

https://kalmanfilter.org/cpp/index.html - Beskrivning och implementering av filtret i C++.

https://commons.apache.org/proper/commons-math/javadocs/api-3.6.1/org/apache/commons/math3/filter/KalmanFilter.html - Beskrivning och implementation av filtret i Java.

https://filterpy.readthedocs.io/en/latest/kalman/KalmanFilter.html - Beskrivning och implementering av filtret i Python

Slutsats

Extended Kalman Filter (EKF) är ett kraftfullt verktyg för att uppskatta tillståndet hos dynamiska system, särskilt när denna uppskattning behöver baseras på data från flera sensorer samtidigt. En av de viktigaste fördelarna med EKF är dess förmåga att integrera information från olika källor, vilket gör det exceptionellt användbart i komplexa system som fordonsnavigeringssystem, robotteknik eller rymdteknik.

Med tanke på högljudda och ofta ofullkomliga data från olika sensorer är EKF kapabel att sammanfoga dessa data till en enhetlig helhet, vilket ger en mer exakt och tillförlitlig uppskattning av tillståndet. Till exempel, i en bil, kan EKF använda GPS-data för att bestämma position och data från en accelerometer för att beräkna hastighet och acceleration, vilket skapar en mer fullständig bild av fordonets rörelse.

Den Utökade Kalmanfiltret (EKF) kan minska den totala osäkerheten som uppstår på grund av brus och fel från varje enskild sensor. Eftersom dessa fel ofta är okorrelerade, möjliggör deras gemensamma behandling i EKF mer stabila och precisa uppskattningar. Det är även värt att notera att EKF uppvisar hög robusthet: vid problem med en av sensorerna kan systemet fortsätta att fungera genom att förlita sig på data från de återstående. Detta gör EKF särskilt värdefullt i kritiska tillämpningar där tillförlitlighet och noggrannhet är av yttersta vikt. En annan viktig aspekt när man arbetar med flera sensorer är tidssynkronisering av mätningar. EKF hanterar skickligt dessa temporala skillnader och säkerställer korrekt datafusion.

Tack vare sin förmåga att samla in och analysera information från flera källor är EKF ett ovärderligt verktyg i områden där hög precision i tillståndsuppskattning krävs under förhållanden av osäkerhet och dynamiska förändringar.

Sammanfattningsvis är mjukvara som bekämpar sensorns brus en svår process som omfattar statiska, statistiska metoder och tillämpningen av artificiell intelligens för klassificering och reduktion av brustyper.

Vårt företag har omfattande expertis i att hantera problem med sensorsus.

För förfrågningar gällande denna artikel, tveka inte att kontakta oss på articles@stofu.io.

För samarbetsmöjligheter kan du kontakta oss på info@stofu.io.

Alla kodfiler hittar du i vårt repository: https://github.com/SToFU-Systems/EKF_Usage.

Önskar dig allt det bästa,

SToFU Systems Team

https://stofu.io

Programvaruansats för att hantera ljud från ADAS-sensorer (Del 1)

Vad är ADAS?

Sensorbrus i ADAS

Simulering av punktrörelse i ett endimensionellt koordinatsystem

Kalmanfiltret

Extended Kalman Filter (EKF)

Ytterligare material

Slutsats

Kategorier

Senaste nyheter

Programvaruansats för att hantera ljud från ADAS-sensorer (Del 1)

PE-resurstolk i C++ (Nativ)

Introduktion till utveckling av Windows-kärnan på Rust (Del 1)

Introduktion till GPU-programmering

Inuti BlackMatter: Teknisk analys av BlackMatter Ransomware